2 Künstliche Neuronale Netze

Inhaltsverzeichnis für dieses Kapitel, für das gesamte Dokument;

2.1 Überblick

Kaum ein anderes Wissenschaftsfeld hat in den letzten Jahren so viel Interesse auf sich gezogen, wie die Künstlichen Neuronalen Netze (KNN). Dabei ist es nach raschen anfänglichen Erfolgen in den 50er Jahren lange Zeit still um sie gewesen. Erst zu Beginn der achtziger Jahre erfuhren sie dank den Entwicklungen von HOPFIELD [7] und KOHONEN [9] eine Renaissance. Der von RUMELHART et al. 1987 vorgestellte Backpropagation-Algorithmus [20] verhalf den KNN zu ihrem Durchbruch. Sprunghaft entstand eine unüberschaubare Anzahl an möglichen Anwendungen künstlicher neuronaler Netze.

Allen Netzmodellen gemein ist das Grundelement, das Neuron. Ein KNN erhält man durch Verschalten mehrerer identischer Neuronen. Dies ergibt eine Netztopologie, die zusammen mit der Arbeitsweise der Neuronen die Funktionalität des KNN bestimmt. Die Benutzung künstlicher neuronaler Netze geschieht in zwei Schritten: Bevor eine Abfrage ein "sinnvolles" Ergebnis liefert, wird das KNN anhand von Beispielen trainiert.

2.2 Das Neuron als informationsverarbeitendes Element

2.2.1 Ein abstraktes Modell

Die ursprüngliche Motivation der Erforschung der KNN war ein besseres Verständnis der Zusammenhänge des Nervensystems. Mit künstlichen neuronalen Netzen wurden biologische neuronalen Netze als informationsverarbeitende Systeme modelliert. Wesentliche Eigenschaften biologischer Nervenzellen dienten als Vorbild bei dem Entwurf künstlicher Neuronen.

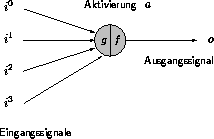
Ein derartiges Neuron besitzt folgenden grundlegenden Aufbau:

Abbildung 2.1: Ein generisches Neuron

• Mehrere Eingangskanäle, über die externe Signale $i^0^,\; ...,\; i^n-1^$ empfangen werden. Die eingehenden Signale werden in der Regel zu einem Vektor zusammengefaßt.
• Das eigentliche Berechnungselement, welches in einem zweistufigen Verfahren zunächst die Aktivierung bestimmt und diese in ein Ausgangssignal transformiert.
• Ein Ausgangskanal, über den das Ausgangsignal zu den Eingangskanälen anderer Neuronen gelangen kann.

Der Informationsfluß in einem künstlichen Neuron beginnt mit der Reduktion des Eingangsvektors zu einem skalaren Wert, der Aktivierung. Diese Reduktion vollzieht sich mit Hilfe einer sogenannten Integrationsfunktion g, welche im einfachsten Fall die Argumente aufaddiert:

$a\; :=\; g(i^0^,\; ...,\; i^n-1^)\; \; =\; \; i^0^\; +\; ...+\; i^n-1^$

Die Aktivierungsfunktion bzw. Transferfunktion f liefert das Ausgangssignal:

$o\; :=\; f(a)\; \; =\; \; f(g(i^0^,\; ...,\; i^n-1^))$

Hierfür wird oft die die sogenannte Treppenfunktion verwandt:

Das Ausgangssignal kann sowohl Eingangssignal für weitere Neuronen sein, als auch über eine Rückkopplung dem Neuron selbst wieder zur Verfügung stehen.

2.2.2 Das McCulloch-Pitts Neuron

Die ersten veröffentlichten Arbeiten auf dem Gebiet der KNN stammen von MCCULLOCH und PITTS [10]. Sie stellten zu Beginn der vierziger Jahre ein Netz vor, dessen Neuronen aus binären Schaltelementen bestanden. Die Signale, die ein solches Neuron verarbeitet, sind somit auch binärer Natur.

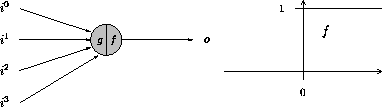
Abbildung 2.2: Ein Neuron von MCCULLOCH und PITTS

Zur Berechnung der Aktivierung wird zusätzlich ein sogenannter Schwellwert $\theta$ herangezogen:

$g(i^0^,\; ...,\; i^n-1^)\; \; :=\; \; i^0^\; +\; ...\; +\; i^n-1^\; -\; \theta$

Die Ausgabe errechnet sich wie folgt:

Ein derartiges Neuron kann bereits einfache boolesche Funktionen wie OR () oder AND ($\theta =n$) berechnen.

2.2.3 Heutige Neuronen

Ausgehend von dem Modell von MCCULLOCH und PITTS wurden Versuche unternommen, die Funktionalität eines Neurons zu erweitern. Die wesentliche Beschränkung, nur binäre Signale zuzulassen, kann wegfallen, wird statt der Treppenfunktion eine sogenannte Sigmoide zur Transformation verwandt:

$f\_T\_(x)\; \; :=\; \{11+e^-\{xT\}^\}$

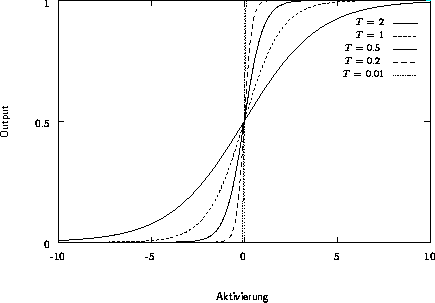
Abbildung 2.3: Sigmoide Funktionenschar

Durch den Parameter T läßt sich die Steigung der Funktion variieren. Große Werte für T haben einen relativ flachen Verlauf zur Folge, während kleine Werte zu einem der Treppenfunktion ähnlichen Graph führen. Abbildung 2.3 zeigt die Funktionsgraphen für verschiedene T.

Ein entscheidender Vorteil dieser Klasse von Transferfunktionen ist die Differenzierbarkeit. Damit kann eine Vielzahl von Verfahren der nichtlinearen Optimierung Anwendung bei den KNN finden. Ein prominentes Beispiel ist der in Abschnitt 3.3 vorgestellte Backpropagation-Algorithmus, der Information über die Ableitung von f benötigt.

Zwei andere häufig verwendete Aktivierungsfunktionen sind der Tangens hyperbolicus und der logistische Sinus. Ihre Funktionsgraphen ähneln dem der Sigmoiden, auch sind sie beide differenzierbar.

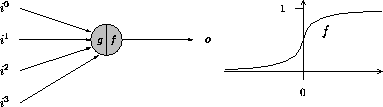
Abbildung 2.4: Ein "modernes Neuron"

Das in Abbildung 2.4 dargestellte Neuron verarbeitet Signale aus dem reellen Intervall $]0,1[$. Dies erleichtert enorm die Kodierung der Problemstellung, da Werte, statt sie in mehrere binäre Signale zu wandeln, nur noch skaliert werden müssen.

2.3 Kopplung von Neuronen: Ein künstliches neuronales Netz

2.3.1 Grundlegende Funktionsweise

Ein KNN ist eine Menge von gleichartigen Neuronen, die über gewichtete Verbindungen miteinander vernetzt sind. Dargestellt wird die Topologie als Graph, wobei die Knoten die Neuronen, die Kanten die Verbindungen repräsentieren. In der Regel sind die Verbindungen bidirektional, d.h. sie fungieren beidermaßen als Eingabe- und Ausgabekanal.

Soll nun für ein gewisses Neuron k der Ausgabewert $o\_k\_$ bestimmt werden, so berechnen sich dessen Eingabewerte $i^j^\_k\_$ aus der Ausgabe $o\_j\_$ aller mit k verbundenen Neuronen, jeweils multipliziert mit dem Gewicht der Verbindung von j nach k, $w\_kj\_$ (siehe Abbildung 2.5):

$i^j^\_k\_\; \; =\; \; w\_kj\_\; o\_j\_$

Der Ausgabewert für Neuron k berechnet sich als:

$o\_k\_\; =\; f(a\_k\_)\; \; =\; \; f(g(w\_k0\_\; o\_0\_,\; ...,w\_kn-1\_\; o\_n-1\_\; ))$

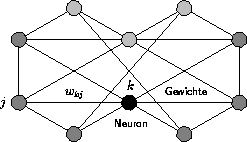
Abbildung 2.5: Darstellung der Topologie eines KNN

Der Vektor aller Ausgabewerte $o\_j\_$ wird als Netzzustand bezeichnet. Bevor ein KNN in Betrieb gesetzt wird, erhalten die Neuronen initiale Ausgabewerte. Dieser Netzzustand stellt die Eingabe an das Netz dar und ist Ausgangspunkt einer Abfrage.

Der weitere Ablauf hängt von der Dynamik des Netzes ab. Im synchronen Modus führen alle Neuronen im Gleichtakt ihren Berechnungen aus. In der Regel steht das Resultat nach einem derartigen Schritt fest, der Netzzustand repräsentiert die Ausgabe des KNN.

Im Gegensatz dazu spricht man von einem asynchronen Betrieb, wenn jeweils nur ein Neuron ausgewählt wird, seinen Ausgabewert zu berechnen. Diese Vorgehensweise benötigt mehrere Schritte, bis ein Ergebnis feststeht. Erst wenn keines der Neuronen mehr seinen Ausgabewert ändert, hat das Netz einen stabilen Zustand erreicht.

Mitunter besitzen nicht alle Neuronen eines KNN die gleiche Funktionalität. Beispielsweise führen Eingabeneuronen keine Berechnungen aus, sondern bekommen einen Wert zugewiesen, den sie als ihren Ausgabewert anderen Neuronen zur Verfügung stellen. Dementsprechend reduziert sich die Dimension des Eingabevektors auf die Anzahl der Eingabeneuronen. Eine Verkleinerung des Ausgabevektors erhält man durch Kennzeichnung gewisser Neuronen als Ausgabeneuronen, ohne allerdings ihre Funktion einzuschränken.

Zu einer vollen Beschreibung eines KNN gehören neben der Topologie des Netzes auch Angaben zu

• der Charakteristik der verwandten Neuronen:
  • Integrationsfunktion g: Sie gibt Aufschluß darüber, ob das Neuron mit einem Schwellwert arbeitet oder nicht.
  • Transferfunktion f: Aus ihr ergibt sich die Art der verarbeiteten Signale.
  • Verwendung von Eingabe- bzw. Ausgabeneuronen
• der Dynamik des Netzes: synchroner bzw. asynchroner Betrieb.
• den zur Verfügung stehenden Trainingsverfahren.

Aufgrund der beinahe unüberschaubaren Vielfalt von KNN, würde eine tiefergehende Betrachtung den Rahmen dieser Arbeit sprengen. Für einen umfassenden Überblick der verschiedenen KNN Architekturen sei auf [6] und [18] verwiesen.

2.3.2 Training künstlicher neuronaler Netze

Ein Grund für den häufigen Einsatz auf KNN basierender Anwendungen [26] ist die Art und Weise, wie Probleme modelliert werden. Es ist zwar hilfreich, aber nicht notwendig, Annahmen bezüglich der Modellzusammenhänge zu treffen. Statt dessen reicht es aus, Daten zu beschaffen, die das Problem exemplarisch beschreiben.

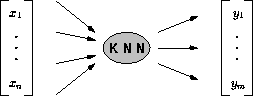
Abbildung 2.6: Informationsfluß in einem KNN

Eine abstrakte Sichtweise des Informationsfluß in einem KNN zeigt Abbildung 2.6. Ein KNN bildet einen n-dimensionalen Vektor x auf einen Vektor y der Dimension m ab. Hierbei sind die Berechnungen, die im Innern des KNN passieren, für den Anwender nicht von Belang.

Das Training künstlicher neuronaler Netze beinhaltet die Anwendung eines Lernverfahrens auf die zur Verfügung stehende Datenmenge. Steht die Problemlösung für die bekannten Daten a priori gar nicht fest (z.B. die Herausbildung von Merkmalen zur Segmentierung einer Menge von Daten), so wird das KNN mit einem unüberwachten Lernverfahren trainiert. Sind dagegen die Beispiellösungen bekannt, so kann zu jeder Eingabe explizit der Fehler berechnet werden, der in das weitere Training einfließt. Diese Methode wird als überwachtes Lernen bezeichnet.

Ein klassisches Problem hierfür, das exklusive Oder (XOR) wird folgendermaßen für den in Abschnitt 6 vorgestellten Simulator bp beschrieben:

## XOR Problem
##
## Wahrheitstabelle:
##
##        | 0 1
##      --|----
##      0 | 0 1
##      1 | 1 0
##        
# pairs=      4
# genpairs=   0
# inputsize=  2 
# outputsize= 1 
0 0, 0;
0 1, 1;
1 0, 1;
1 1, 0;

Für dieses Problem ist der Eingabevektor x zweidimensional, der Ausgabevektor y eine skalare Größe. Zwei miteinander assoziierte Vektoren x,y heißen Trainingspaar.

Wird ein KNN zur Approximation eigesetzt (siehe Abschnitt 3.5), so ist das Ziel des Trainings ein KNN, welches für jedes Paar $(x,y)$ bei Eingabe von x ein Resultat $y\text{'}$ nahe dem Sollwert y ausgibt. Nahe deshalb, weil ein exaktes Ergebnis gar nicht im Vordergrund steht, sondern vielmehr die Fähigkeit des KNN zur Generalisierung, welche erfahrungsgemäß mit einer zu genauen Reproduktion verloren geht.

Generalisierung bedeutet in diesem Zusammenhang, daß das KNN einem nicht trainierten Eingabevektor einen Ausgabevektor zuordnet, den der Anwender als "sinnvoll" erachtet. In diesem Fall hat das KNN durch das Training die den Beispielen immanenten Zusammenhänge gelernt, die dem Anwender auf den ersten Blick verborgen bleiben.

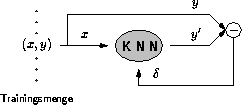
Abbildung 2.7: Überwachtes Lernen in einem KNN

Der eigentliche Lernvorgang geschieht durch Anpassung der Verbindungsgewichte und, falls vorhanden, der Schwellwerte anhand der vom KNN produzierten Fehler (siehe Abbildung 2.7). Für jedes Trainingspaar $(x,y)$ wird zu dem Eingabevektor x die Ausgabe des KNN $y\text{'}$ berechnet. Die Abweichung $\delta$ vom Sollwert y fließt in die Korrektur der Gewichte ein. Gesucht ist eine Konstellation, die den Fehler über alle Trainingspaare, die die Trainingsmenge bilden, minimiert. Das einmalige Präsentieren aller Trainingspaare mit anschließendem Aktualisieren der Gewichte wird als Epoche bezeichnet. Ob das KNN nur "auswendig" gelernt hat, zeigt sich nach dem Training bei dem Generalisierungstest, der Validierung. Die Testmenge enthält vorhandene aber nicht trainierte Paare, die dem KNN präsentiert werden. Die hierbei beobachtete Abweichung ist ein verläßlicheres Maß für den Lernerfolg als allein der Fehler auf der Trainingsmenge.