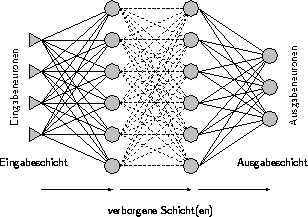
Abbildung 3.1: Topologie eines MP-Netzes
Inhaltsverzeichnis für dieses Kapitel, für das gesamte Dokument;
Das Mehrschicht Perzeptron Netz (MP-Netz) gehört aufgrund seiner Flexibilität zu den am häufigsten eingesetzten KNN [26], da es sich sowohl zur Klassifikation als auch zur Funktionsapproximation eignet. Gerade letztere Eigenschaft macht das MP-Netz zur Prognose von Zeitreihen interessant, da konventionelle Methoden ein immenses Fachwissen voraussetzen, um Annahmen bezüglich der Modellparameter treffen zu können.
Im folgenden Kapitel wird neben den Grundlagen des MP-Netzes ausführlich auf ein Verfahren zum Training von MP-Netzen, den Backpropagation-Algorithmus, eingegangen. Eine Erweiterung des Verfahrens, welche während des Trainings dem Netz Neuronen hinzufügt, wird vorgestellt. Zum Abschluß werden die Grundzüge der Zeitreihenprognose mit MP-Netzen erläutert.
Das Mehrschicht Perzeptron Netz gehört zur Kategorie der vorwärtsgerichteten KNN. Diese Netztopologie zeichnet sich durch einen kreisfreien Graphen aus, dessen Kanten gerichtet sind. Es wird somit zwischen eingehenden (rezeptiven) und ausgehenden (projektiven) Verbindungen unterschieden.
Die Neuronen eines MP-Netzes sind, ihrer Funktionalität entsprechend, hierarchisch in Schichten angeordnet. Neuronen, die keine rezeptiven Verbindungen besitzen, werden zur Eingabeschicht zusammengefaßt, Neuronen ohne projektive Verbindungen bilden die Ausgabeschicht. Neuronen, die sich zwischen diesen zwei Schichten befinden, werden verborgene Neuronen genannt und sind in einer oder mehreren verborgenen Schichten organisiert. Verbunden sind ausschließlich Neuronen zweier benachbarter Schichten. Abbildung 3.1 zeigt ein MP-Netz. Die Eingabeneuronen sind, da sie keine Berechnungen ausführen, anders dargestellt: Pfeile deuten die Orientierung der Kanten an.

Abbildung 3.1: Topologie eines MP-Netzes
Die verwendeten Neuronen entsprechen dem in Abschnitt 2.2.3 vorgestellten Typ. Es wird mit Schwellwert gearbeitet. Als Transferfunktion kommt die Sigmoide mit (siehe Abbildung 2.3) zum Einsatz. Die Berechnung der Ausgabewerte geschieht in jeder Schicht synchron, von Schicht zu Schicht sequentiell beginnend mit der ersten verborgenen. Im einzelnen wird die Abfrage des Netzes in Abschnitt 3.3.2 beschrieben.
Der von RUMELHART et al. [20] vorgestellte Backpropagation-Algorithmus gehört zu der Kategorie überwachter Lernverfahren. Der entscheidende Fortschritt ist die Möglichkeit, auch für die verborgenen Neuronen einen Abbildungsfehler und damit Gewichtskorrekturen berechnen zu können. Vom Standpunkt der nichtlinearen Optimierung her betrachtet, entspricht der Backpropagation-Algorithmus dem Gradientenabstieg, angewandt auf die Besonderheiten eines MP-Netzes [1].
Das Training eines MP-Netzes mit dem Backpropagation-Verfahren beginnt mit der Initialisierung der Gewichte und Schwellwerte mit Zufallwerten aus dem Intervall . Der eigentliche Algorithmus gliedert sich in zwei sich abwechselnde Schritte. Das Resultat eines Eingabevektors wird in der Forward-Phase berechnet. Die Backward-Phase dient dazu, den Abbildungsfehler und damit die Gewichtskorrektur für jede Schicht zu bestimmen. Das Anwenden des Backpropagation-Algorithmus auf alle Trainingspaare wird als Epoche bezeichnet. Durch wiederholtes Trainieren stellt sich eine fehlerminimierende Konstellation der Gewichte ein.
Ausgehend von der ersten verborgenen Schicht werden die jeweils neuen Ausgabewerte für eine Schicht berechnet. Ein Neuron benötigt hierfür die Ausgabewerte der Vorgänger sowie die Gewichte der rezeptiven Kanten.
Neuron k in Abbildung 3.2 führt folgende Operationen aus:
Diese Schritte können für alle m Neuronen unabhängig voneinander ausgeführt werden. Die für Neuron k relevanten Gewichte befinden sich in der k-ten Zeile der Gewichtematrix. Im wesentlichen entspricht die Bestimmung der Aktivierung für alle Neuronen der Schicht einer Multiplikation der Matrix mit dem Vektor der Ausgabewerte der Schicht .
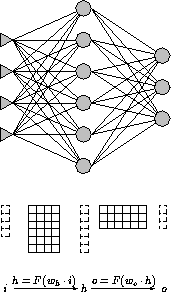
Abbildung 3.3: Matrix-Vektor-Operationen in der Forward-Phase
Abbildung 3.3 stellt die Gesamtsicht für ein dreischichtiges MP-Netz dar. Die Benennung der Schichten orientiert sich an ihrer Funktionalität: input, hidden und output. Die Schwellwerte können als zusätzliche Gewichte zu einem Neuron mit einer konstanten Aktivierung von 1 aufgefaßt werden. Die Abbildung ist eine vektorielle Verallgemeinerung der Transferfunktion f. Das Resultat für einen Eingabevektor x berechnet sich wie folgt:
Die zweite Phase des Backpropagation-Algorithmus dient zur Korrektur der Verbindungsgewichte. Hierfür wird an den Neuronen der Ausgabeschicht das Resultat der Eingabe x mit dem Sollwert y verglichen. Die Differenz ergibt den Fehler des jeweiligen Ausgabeneurons:
Die Bestimmung des Fehlers der verborgenen Neuronen basiert auf der Rückverfolgung des Fehlers der Ausgabeschicht, da auch verborgene Neuronen ihren Anteil am Zustandekommen des Ergebnisses haben. Neuron j in Abbildung 3.4 benötigt dazu die Fehlerwerte seiner Nachfolger und die Gewichte der projektiven Kanten. Der Fehler für verborgene Neuronen berechnet sich als:
Die Identität gilt für die Sigmoide als Transferfunktion und erleichtert die Berechnungen, da die Ausgabewerte noch aus der Forward-Phase stammen. Die Bestimmung der Fehlerwerte endet bei der ersten verborgenen Schicht, da Eingabeneuronen keine Berechnungen ausführen.
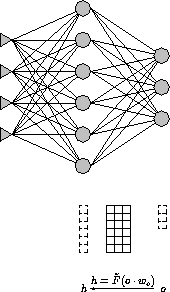
Abbildung 3.5: Vektor-Matrix-Operationen in der Backward-Phase
Analog zur Forward-Phase ist ein Teil der Berechnungen, die zur Berechnung des Fehlers verborgener Neuronen dienen, als Multiplikation der transponierten Gewichtematrix mit dem Fehlervektor anzusehen. Diese Vektor-Matrix-Operation stellt Abbildung 3.5 dar, wobei o den Fehlervektor der Ausgabeschicht, h den der verborgenen Schicht bezeichnet.
Die Gewichtsänderungen nehmen die Neuronen bezüglich der rezeptiven Kanten auf ihrer Eingangsseite vor. Die Änderungen berechnen sich gleichermaßen für verborgene Neuronen und Ausgabeneuronen:
Der Faktor wird als Lernrate bezeichnet und gibt die Schrittweite des Gradientenabstiegs an. Üblicherweise wird für ein Wert zwischen null und eins gewählt, der während des Trainings für alle Neuronen gleich bleibt. Ein optimaler Wert kann a priori nicht angegeben werden, sondern sich nur durch Experimente herausstellen.
Ein Problem aller Gradientenverfahren stellt die Existenz lokaler Minima der zu minimierenden Funktion dar. Häufig kommt die Suche in einem Suboptimum zum Stehen. Um dem vorzubeugen bietet der Backpropagation-Algorithmus einige Parameter, die es erlauben, den Gradientenabstieg zu manipulieren.
Eine der wichtigsten Stellgrößen ist die Lernrate . In der Theorie wird mittels einer hinreichend kleinen Lernrate in jedem Fall das globale Minimum erreicht [6]. Eine kleine Lernrate verlängert die ohnehin langen Trainingszeiten jedoch erheblich.
Einige Verfeinerungen des Backpropagation-Algorithmus versuchen durch Einbeziehung weiterer Informationen als nur des momentanen Gradienten, Aufschluß über die Beschaffenheit der Fehlerfunktion zu gewinnen [1]. Dadurch sollen sich gegenseitig aufhebende und damit unnötige Gewichtsänderungen vermieden werden. Im Vergleich zum ursprünglichen Backpropagation-Algorithmus wird insbesondere bei regelmäßigen Fehlerverläufen ein Optimum in deutlich weniger Schritten erreicht.
Das einfachste Verfahren dieser Art stellt die Verwendung eines Momentums bzw. Impulses dar. Zu der aus den Fehlern der Neuronen resultierenden Gewichtsänderung wird ein Bruchteil der letzten aufaddiert:
Ein optimaler Wert für kann ebenfalls nicht a priori angegeben werden. Er sollte kleiner als eins gewählt werden, da ansonsten der Betrag des Korrekturterms stark anwächst (geometrische Reihe).
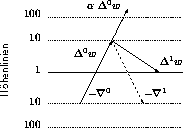
Abbildung 3.6: Gewichtskorrektur mit einer
Impulsrate
von 0.5
Abbildung 3.6 illustriert die Korrektur für ein einfaches Beispiel. Die durchgezogenen Pfeile stellen die realisierten Änderungen der Gewichte dar. Die Änderung geschieht in einer dem Gradienten entgegengesetzten Richtung. Der gestrichelte Vektor entspricht der Änderung ohne Impuls, zusammen mit dem gepunktet dargestellten Momentum ergeben beide die realisierte Korrektur.
Komplexere Verfahren verwenden beispielsweise Methoden zweiter Ordnung, bzw. adaptive Variation der Parameter und . Eine detaillierte Beschreibung der Verfahren findet sich in [1] und [6].
Eine der ältesten Modifikationen des Backpropagation-Algorithmus besteht darin, die während der Backward-Phase berechneten Gewichtsänderungen unmittelbar wirksam werden zu lassen, so daß die neuen Gewichte für das nächste Trainingspaar bereits relevant sind (Online-Training). Demgegenüber bezeichnet das Batch-Training das Akkumulieren der Änderungen über alle Paare der Trainingsmenge. Erst nach einer vollständigen Epoche werden die Gewichte aktualisiert.
Beide Varianten differieren stark sowohl bezüglich der Anzahl der benötigten Epochen, als auch des Trainingsresultats, also der berechneten Gewichte. Außerdem sind die Modifikationen unterschiedlich effektiv. Während die Abfolge der Trainingspaare für das Batch-Training unerheblich ist, ist es für das Online-Training wichtig, daß für jede Epoche die Paare in zufälliger Reihenfolge trainiert werden.
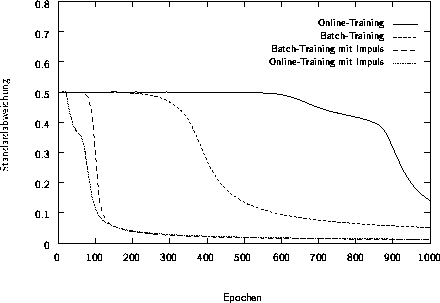
Abbildung 3.7: Fehlerverlauf beim Training des XOR-Problems
Abbildung 3.7 zeigt den Fehlerverlauf während des Trainings des XOR-Problems (siehe Abschnitt 2.3.2) für vier Experimente. Trainiert wurde ein MP-Netz mit zwei Eingabeneuronen, einem Ausgabeneuron und zwei Neuronen in der verborgenen Schicht. Zur Anwendung kamen sowohl das Online- als auch das Batch-Training zum einen mit einer Lernrate von 1.0, zum andern mit einer Lernrate von von 2.0 zusammen mit einer Impulsrate vom 0.9. Es zeigen sich deutliche Unterschiede in der Konvergenzgeschwindigkeit der verschiedenen Ansätze, weshalb eine geeignete Wahl der Lernparameter die Anzahl der erforderlichen Epochen erheblich verkürzt.
Ein wesentliches Problem bleibt allerdings die Tatsache, daß ein kleiner Fehler auf der Trainingsmenge nicht unbedingt mit einem guten Generalisierungsverhalten, also einem kleinen Fehler auf der Testmenge einhergeht. Vielmehr verhält es sich mit beiden Zielen in der Regel gegenläufig, d.h. der Fehler bezüglich der Testmenge steigt während des Trainings an, statt ebenfalls zu sinken. Dieser Effekt wird als Overfitting bezeichnet. Das im folgenden Abschnitt vorgestellte Verfahren versucht, dieses Problem auf einer konstruktiven Art zu beheben.
Trotz ihrer leichten Anwendbarkeit, beherbergen MP-Netze ein hartnäckiges Problem. Zu einer gegebenen Datenmenge eine passende Anzahl verborgener Neuronen anzugeben ist Sache des Anwenders. Die Erfahrung lehrt, daß verhältnismäßig kleine MP-Netze in der Lage sind, wesentliche Merkmale zu extrahieren und somit gut zu generalisieren. Jedoch kann die Trainingsmenge nicht beliebig genau reproduziert werden. Hierfür ist eine größere Anzahl verborgener Neuronen notwendig. Hieraus resultieren allerdings auch MP-Netze mit einer verstärkten Tendenz zum Auswendiglernen der Trainigspaare einhergehend mit unbefriedigender Verallgemeinerungsfähigkeit. Konstruktionsalgorithmen versuchen nun, die positiven Eigenschaften sowohl der kleinen als auch der großen MP-Netze zu vereinigen [27]. Mit einem verhältnismäßig kleinem MP-Netz beginnend werden in der Trainingsphase dem Netz verborgene Neuronen hinzugefügt.
Das hier vorgestellte Verfahren ersetzt während des Trainings in regelmäßigen Abständen ein Neuron durch zwei neue. Dieses Aufspalten wird auf Neuronen angewendet, die durch stark oszillierende Gewichtsänderungen auffallen. Dahinter verbirgt sich die Hoffnung, daß zwei Neuronen die Aufgabe des einen besser erfüllen. Neuronen werden also nur dort zugefügt, wo Bedarf besteht. Ein derartig gewachsenes MP-Netz weist aufgrund seiner Entwicklung ein deutlich besseres Generalisierungsvermögen auf als ein Netz mit einer von Anfang an großen Zahl verborgener Neuronen [5].
Die Ausführungen stützen sich im wesentlichen auf die Arbeit von GLÖCKNER [5]. Ein empirischer Vergleich dieses Algorithmus mit MP-Netzen fester Topologie findet in Abschnitt 3.5.2 statt.
Der Erfolg des MouseProp-Algorithmus hängt entscheidend von den Kriterien ab, die ein aufzuspaltendes Neuron auszeichnen. Ein Maß für die "Oszillation eines Neurons" wird im folgenden Abschnitt vorgestellt.
Während einer Epoche werden die durch den Backpropagation-Algorithmus berechneten Gewichtsänderungen für alle T Trainingspaare protokolliert, um für jede Verbindung von Neuron j zu Neuron k folgende numerischen Größen zu kennen:
Hierbei bezeichnet die absolute Summe und die Summe der absoluten Änderungen von . Ein Wert nahe null für deutet auf sich gegenseitig auslöschende Änderungen hin und entspricht einer hohen Oszillation. Um verschiedene Verbindungen miteinander vergleichen zu können, wird ein normiertes Maß für die Oszillation der Gewichtsänderungen einer Verbindung eingeführt:
Hieraus wird die relative Oszillation eines Neurons j bezüglich seiner projektiven Gewichte abgeleitet, indem über alle Nachfolger k gemittelt wird:
Die relative Oszillation allein ist nicht geeignet, einen Kandidaten aus der Menge aller verborgenen Neuronen zu bestimmen, da für alle Neuronen, die sich in einem Fehlerminimum befinden, eine starke Oszillation der Gewichte beobachtet wird. Deshalb werden nur solche Neuronen in Betracht gezogen, die einen überdurchschnittlichen relativen Fehler aufweisen. Erst aus dieser Menge wird als aufzuspaltendes Neuron das mit der höchsten relativen Oszillation ausgewählt.
Die Änderung der Topologie wirkt sich nur lokal aus und beeinträchtigt nicht das Abbildungsverhalten eines MP-Netzes.
Abbildung 3.8 zeigt die Aufteilung der Gewichte beim Aufspalten eines Neurons j in zwei Neuronen j' und j''. Die Gewichte der rezeptiven Kanten werden dupliziert. Der Vektor der projektiven Gewichte wird so auf die beiden Neuronen aufgeteilt, daß die Summe den ursprünglichen Vektor ergibt. Der jeweilige Anteil wird für alle Komponenten per Zufallsgenerator ermittelt.
Das auf diese Weise entstandene Netz zeigt zum vorhergehenden keine Unterschied bezüglich des Abbildungsverhaltens (monoton). Allein die Fehler der Neuronen j' und j'' entsprechen nicht mehr dem des Originals j (fehlerlokal).
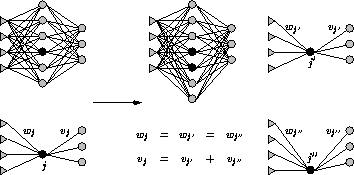
Abbildung 3.8: Aufspalten eines Neurons
Für den Benutzer des MouseProp-Algorithmus kommen zwei weitere Trainingsparameter hinzu, deren optimaler Wert nur experimentell bestimmt werden kann. Die Anzahl der Epochen zwischen zwei Aufspaltungen sollte nicht zu klein bemessen sein, damit die Gewichte Gelegenheit erhalten, sich neu einstellen. Eine zu hohe Anzahl verlangsamt das Training unnötig. Ebenso bleibt die initiale Größe der verborgenen Schicht des MP-Netzes Sache des Anwenders.
Für das Problem, die optimale Netzkonfiguration zu finden, ist dieses Verfahren keine Lösung. Dafür bietet es eine gewisse Stabilität gegenüber Overfitting bei einer großen Anzahl verborgener Neuronen. Außerdem wird das Training im Vergleich zu einem von Anfang an großem MP-Netz beschleunigt. Zum einen dadurch, daß ein Fehlerminimum in weniger Epochen erreicht wird, zum andern benötigt eine Epoche selbst weniger Zeit.
Zur Modellierung einer Problemstellung bieten sich in der Regel mehrere Varianten an. Sie unterscheiden sich zum Beispiel in der Anzahl der einstellbaren Parameter und des Abbildungsfehlers. Welches Modell der wirklichen Situation am ehesten gerecht wird, ist schwer zu entscheiden.
Eine Hilfestellung bietet das Verfahren von SCHWARZ [21]. Es ermittelt für jede Modellvariante einen Koeffizienten, das sbic. Die Formulierung des Schwarz'schen Bayesianischen Informationskriteriums für autoregressive Modelle (siehe Abschnitt 3.5.1) setzt den Modellfehler in Relation zu der Anzahl der Modellparameter und der Anzahl der Datenpunkte:
Das sbic eines Modells steht für dessen Wirklichkeitsnähe, wobei ein kleiner Wert eine hohe Übereinstimmung mit der Realität ausdrückt. Diese Eigenschaft wird in [15] ausgenutzt, um MP-Netze konstanter Topologie mit einer unterschiedlichen Anzahl an verborgenen Neuronen zu vergleichen. Die Anzahl p der Modellparameter berechnet sich als Summe aller Gewichte und Schwellwerte. Der Modellfehler rms (root mean square error) entspricht der Standardabweichung aller n Trainingspaare. In der Regel besitzt das sbic ein einziges globales Minimum, was einer optimalen Netztopologie entspricht.
Das sbic kann somit auch ein Anhaltspunkt dafür sein, ob sich das Hinzufügen eines Neurons nennenswert gelohnt hat. Eine Berechnung des sbic unmittelbar vor jedem Aufspalten erlaubt Rückschlüsse auf den Erfolg der letzten Aufspaltung. Einen beispielhaften Verlauf des sbic während des Trainings mit dem MouseProp-Algorithmus zeigt Abbildung 3.14 in Abschnitt 3.5.2.
Eine Zeitreihe beschreibt die Entwicklung einer Variablen x, die an diskreten Zeitpunkten beobachtet wurde. Ein autoregressives Modell versucht, einen Zusammenhang für aufgrund der Historie abzuleiten:
Ziel ist es, eine geeignete Funktion f zu finden, die für alle bekannten Datenpunkte ein zufriedenstellendes Ergebnis erzielt. Die eigentliche Aufgabe besteht nun darin, den Abbildungsfehler zu minimieren, indem Parameter der Funktion f variiert werden. Am einfachsten gestaltet sich dies für lineare Funktionen. Für sie liefert die Methode der kleinsten Quadrate optimale Werte, jedoch ist das Ergebnis häufig nicht zufriedenstellend, zum Beispiel weil der tatsächliche Zusammenhang nichtlinearer Natur ist.
Eine spezielle Kategorie nichtlinearer Funktionen stellen die MP-Netze dar. Vor allem zeichnen sie sich als universelle Approximatoren aus [8]. D.h. zu jeder Trainingsaufgabe existiert ein MP-Netz, welches nach dem Training mit dem Backpropagation-Algorithmus die Trainingspaare beliebig genau annähert [25].
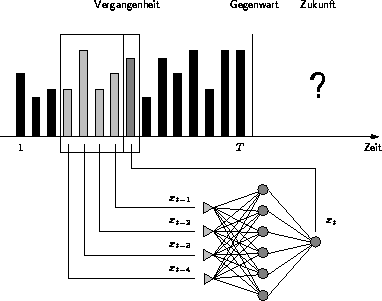
Abbildung 3.9: Zeitreihenprognose mit einem MP-Netz
Die Modellierung eines autoregressiven Prozesses mit Hilfe eines MP-Netzes zeigt Abbildung 3.9. Um den Wert für vorherzusagen, werden die der vorherigen Zeitpunkte der Eingabeschicht präsentiert. Die Ausgabeschicht besteht aus nur einem Neuron und gibt den Wert zum Zeitpunkt t an. Die Prognose des zukünftigen Wertes geschieht durch Eingabe der Werte , , und .
Für den Fall, daß es sich um eine Zeitreihe von Vektoren der Dimension n handelt, besteht die Möglichkeit, jeden Vektor auf n Eingabe- bzw. Ausgabeneuronen abzubilden. In der Praxis wird jedoch ein anderer Weg verfolgt. Um die Komplexität der Trainingsaufgabe eines einzelnen Netzes zu reduzieren, werden n MP-Netze darauf trainiert, jeweils nur eine Komponente des Ergebnisvektors zu prognostizieren.
Die Anzahl der verborgenen Neuronen bleibt Sache des Anwenders. Sie kann beispielsweise mit dem Verfahren aus Abschnitt 3.4.5 optimiert werden.
Zusätzliche Einflußfaktoren neben der eigentlichen Zeitreihe werden miteinbezogen, indem sie auf weitere Eingabeneuronen abgebildet werden. Ein MP-Netz ist in der Lage, die Relevanz der Informationen zu erkennen und sie zu berücksichtigen bzw. sie zu ignorieren. Allerdings ist es hilfreich, die Eingabedaten in einer Vorverarbeitung auf redundante Elemente hin zu untersuchen und mit diesen Anhaltspunkten die Trainingsmenge nominell zu verkleinern.
In dem folgenden Abschnitt wird die Prognose einer "synthetischen" Zeitreihe untersucht. Die der Zeitreihe zugrundeliegenden Daten werden aus der VERHULST-Gleichung generiert:
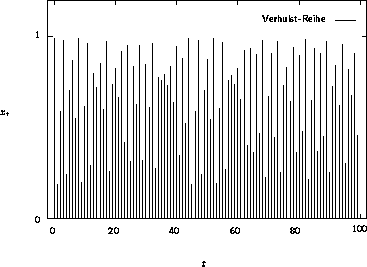
Abbildung 3.10: Eine VERHULST-Reihe
Bekannter als die Gleichung selbst, dürfte das FEIGENBAUM-Diagramm sein, welches für wechselnde Parameter k die zugehörigen Fixpunkte angibt [17]. Werte um 3,8 für k führen zu einem Verhalten, welches als deterministisches Chaos bezeichnet wird. Die aus der VERHULST-Gleichung generierte Zeitreihe weist in diesem Bereich eine große Ähnlichkeit mit einem Zufallsprozeß auf. Einem Betrachter der Zeitreihe offenbart sich nicht der doch einfache Zusammenhang (siehe Abbildung 3.10).
Es werden drei MP-Netze mit einer unterschiedlichen Anzahl verborgener Neuronen trainiert. Die Problemstellung ist für alle drei gleich. Bei Eingabe der letzten drei Werte der Zeitreihe soll der nächste ausgegeben werden. Hieraus resultieren drei Eingabe- und ein Ausgabeneuron. Die Zahl der verborgenen Neuronen beträgt einmal sechs, einmal 24. Für das dritte Netz wird der MouseProp-Algorithmus angewendet. Die verborgene Schicht umfaßt zu Beginn des Trainings sechs, danach 24 Neuronen.
Um mit dem verarbeiteten Signaltyp kompatibel zu sein, sind die Daten der Zeitreihe so skaliert, daß nur Werte aus dem Intervall [0,1] angenommen werden. Die Trainingsmenge besteht aus 31 Paaren, die Testmenge aus 7 Paaren.
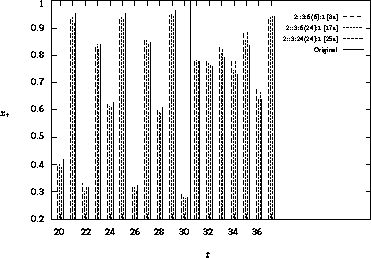
Abbildung 3.11: Prognose einer VERHULST-Reihe
Nach 4000 Epochen wird für jedes Netz eine Abfrage durchgeführt. Abbildung 3.11 zeigt für jedes MP-Netz den Prognosewert. Die jeweils rechte Säule gibt zum Vergleich den Originalwert an. Die Netztopologie wird nach folgendem Muster beschrieben:
<Anzahl der aktiven Schichten>:
:<Anzahl der Eingabeneuronen>
:<initiale Anzahl verborgener Neuronen>
(<maximale Anzahl verborgener Neuronen>)
.
.
.
:<Anzahl der Ausgabeneuronen>
In den eckigen Klammern neben der Netztopologie ist die Dauer des Trainings angegeben.
Offensichtlich sind alle MP-Netze in der Lage, die Trainingsaufgabe zu reproduzieren. Doch zeigen sich auf der Testmenge () deutliche Unterschiede. Hier schneidet das Netz, welches mit dem MouseProp-Algorithmus trainiert wurde, am besten ab.
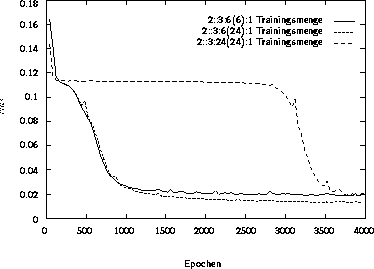
Abbildung 3.12: Fehlerverlauf auf der Trainingsmenge
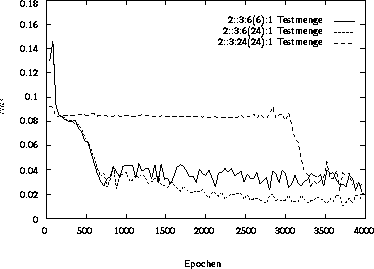
Abbildung 3.13: Fehlerverlauf auf der Testmenge
Als sehr aufschlußreich zeigt sich die Verfolgung
des Fehlers auf der Trainingsmenge (Abbildung 3.12)
und der Testmenge (Abbildung 3.13).
Auffällig ist hier, daß das
kleine (2::3:6(6):1) und
das mittlere (2::3:6(24):1) Netz
bereits nach rund 1000 Epochen Fehlerwerte
in der Nähe eines Minimums erreicht haben.
Für das große Netz (2::3:24(24):1)
ist dies erst nach 3500 Epochen der
Fall. Der verhältnismäßig späte Abbruch
des Trainings für das kleine und mittlere Netz
führt nicht zu einem Overfitting.
Das kleine MP-Netz profitiert allerdings
auch nicht von der langen Trainingsdauer, da
es eine anhaltend starke Oszillation des Fehlers
der Testmenge bei gleichbleibend
hohem Niveau aufweist.
Insgesamt gesehen zeigt sich das mittlere MP-Netz
als die beste Wahl. Es schlägt die anderen beiden
sowohl bezüglich der Anzahl der Epochen als auch
des erreichten Fehlerminimums.
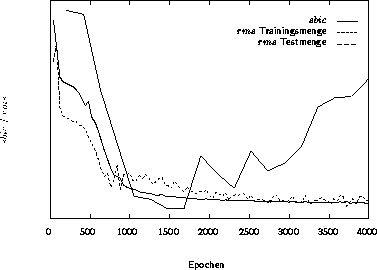
Abbildung 3.14: Verlauf des sbic während des Trainings
Soll für das mittlere MP-Netz eine optimale Zahl der verborgenen Neuronen gefunden werden, so bietet das sbic eine Hilfestellung. Abbildung 3.14 stellt die Entwicklung des sbic zusammen mit dem Fehlerwert rms für das mit dem MouseProp-Algorithmus trainierte MP-Netz dar. Vor jedem Aufspalten wird der sbic berechnet und ausgegeben. Der minimale Wert des Kriteriums liegt hier bei 1500 Epochen, welches einer Anzahl von 13 verborgenen Neuronen entspricht. Dieser Wert ist allerdings abhängig von der Anzahl der Epochen zwischen zwei Aufspaltungen.
Das Abfallen des sbic in der ersten Hälfte des Trainings ist im wesentlichen auf die starke Reduzierung des Fehlers zurückzuführen. Der Anstieg in der zweiten Hälfte des Trainings deutet darauf hin, daß die Aufnahme zusätzlicher Neuronen den Fehler nicht im gleichen Maße herabsenken kann.
In Abschnitt 3.5.2 wird gezeigt, daß MP-Netzen der funktionale Zusammenhang einer chaotischen Zeitreihe antrainiert werden kann. Die Prognose von Zeitreihen, wie sie in der Wirklichkeit auftreten, findet nach dem gleichen Prinzip statt. Unterstützend kommt hinzu, daß MP-Netze in der Lage sind, aus verrauschten Trainingsdaten, die deterministische Komponente zu extrahieren [15].
Die zu prognostizierende Variable ist in vielen Fällen Bestandteil eines größeren Systems, dessen Grenzen schwer abzustecken sind. Häufig werden MP-Netze im wirtschaftlichen Bereich eingesetzt, da dort auf eine lange Erfahrung auf dem Gebiet der Modellierung zurückgegriffen werden kann und umfassende Datenmengen vorliegen [24].
Aus der Berücksichtigung vieler Erklärungsgrößen neben der eigentlichen Zeitreihe resultieren verhältnismäßig große Netze und umfangreiche Trainingsmengen. Beides führt zu einer langen Trainingsdauer, die sich im Bereich von einigen Stunden bewegt. Eine Möglichkeit, diese Zeit zu verkürzen, bietet die Parallelisierung des Backpropagation-Algorithmus, welche im folgenden Kapitel ausführlich behandelt wird.