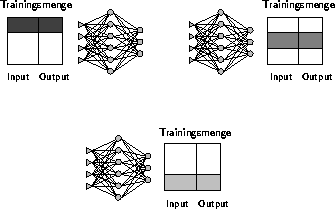
Abbildung 4.1: Paralleles Batch-Training : Trainingsphase
Inhaltsverzeichnis für dieses Kapitel, für das gesamte Dokument;
Die langen Laufzeiten des Backpropagation-Algorithmus signifikant zu verkürzen ist das Ziel einer effizienten Parallelisierung. Nach der Vorstellung grundlegender Konzepte paralleler Systeme werden mögliche Strategien zur Aufteilung des Trainings und dessen paralleler Abarbeitung präsentiert. Die Implementation für das Parallelrechnerbetriebssystem PARIX und das Message-Passing-Modell PVM werden vorgestellt und zum Abschluß deren Effizienz für verschiedene Architekturen verglichen.
Das Konzept jeder Art von Parallelrechner ist die Verwendung vieler (kleiner) Prozessoreinheiten, die zusammengenommen mehr leisten als ein zentraler Hochleistungsprozessor. Ein großer Vorteil paralleler Systeme ist ihr nahezu lineares Preis/Leistungsverhältnis, was für Ein-Prozessor-Maschinen vergleichbarer Rechenleistung nicht besteht. Die Nutzbarmachung des Verarbeitungspotentials eines parallelen Rechners ist allerdings von der Formulierung effizienter paralleler Algorithmen abhängig.
Wesentliche Unterscheidungsmerkmale paralleler Rechner sind neben der Prozessorhardware die Kontrolle der Programmausführung und die Art der Speicherorganisation. Ein SIMD-Rechner (single instruction, multiple data) zeichnet sich durch die synchrone Programmausführung aus. Auf allen Prozessoren wird zur gleichen Zeit der gleiche Programmcode auf unterschiedliche Daten angewendet. Demgegenüber charakterisiert das MIMD-Modell (multiple instruction, multiple data) einen Rechner, dessen Prozessoren unterschiedliche Programme ausführen und auf lokalen Daten operieren. Erhält jeder Prozessor eines MIMD-Rechners das gleiche Programm, so entspricht dies dem SPMD-Modell (single program, multiple data).
In der Regel erfordet die parallele Abarbeitung eines Problems den Austausch von Daten (zum Beispiel Teilergebnisse) unter den Prozessoren. Wird der zur Verfügung stehende Speicherplatz global verwaltet (shared memory), so hat jeder Prozessor Zugriff auf jeden Bereich des Speichers. Der Informationsaustausch findet über den gemeinsamen Speicher statt. Interprozessorkommunikation ist dann erforderlich, wenn jeder Prozessor seinen eigenen lokalen Speicherbereich (distributed memory) besitzt. Informationen werden als Nachrichten unter den Prozessoren ausgetauscht (message passing). Sowohl gemeinsamer Speicher als auch message passing erfordert ein Verbindungsnetzwerk unter den Prozessoren.
Neben massiv parallelen Systemen mit bis zu tausend Prozessoren werden inzwischen auch vermehrt vernetzte UNIX-Workstations zur Parallelverarbeitung eingesetzt. Obwohl spezielle Parallelrechner bessere Voraussetzungen beispielsweise bei der Kommunikation bieten, besitzt ein Workstationverbund den Vorteil, daß die benötigte Hardware bereits vorhanden und durch den alltäglichen Gebrauch kaum ausgelastet ist.
Das Training eines MP-Netzes mit dem Backpropagation-Algorithmus bietet mehrere Ansätze der Parallelisierung. Der vermutliche einfachste Weg verfolgt die Idee, völlig verschiedene, voneinander unabhängige Experimente auf die Prozessoren zu verteilen.
Die Parameter eines Experiments sind beispielsweise die Netztopologie, die Trainingsmuster und Lernparameter. Dieser Ansatz erfordert kaum Kommunikation, auf jedem Prozessor des Parallelrechners läuft der sequentielle Algorithmus. Diese Idee ist jedoch untauglich, falls die Experimente in einer bestimmten Reihenfolge ablaufen sollen.
Die Evolution optimaler MP-Netze hinsichtlich ihrer Topologie und ihrer Gewichte mit Hilfe genetischer Algorithmen macht sich diesen Ansatz zunutze [2].
Eine grobkörnige Parallelisierung bietet das Unterteilen der Trainingsmenge in gleichmäßige Stücke. Auf allen Prozessoren befindet sich eine identische Kopie des MP-Netzes. Nachdem jeder Prozessor den Backpropagation-Algorithmus auf seine lokale Trainingsmenge angewendet hat, werden die gesammelten Gewichtskorrekturen untereinander ausgetauscht. Auf diese Art läßt sich das Batch-Training (siehe Abschnitt 3.3.4) vor allem für große Trainingsmengen sehr effektiv parallelisieren [3],[13], da nur einmal pro Epoche kommuniziert wird.

Abbildung 4.1: Paralleles Batch-Training : Trainingsphase
Die lokalen Gewichtsänderungen addieren sich zu der globalen Gewichtsänderung auf. Diese erhält jeder Prozessor zurück und kann damit seine Kopie des MP-Netzes aktualisieren.
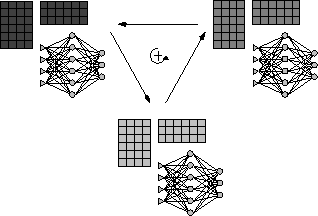
Abbildung 4.2: Paralleles Batch-Training : Angleichen der Gewichte
Die Trainingspaare werden zu Programmbeginn den Prozessoren zugeteilt. Während des Trainings erfolgt keine Neuverteilung, da die jeweilige Prozessorlast konstant bleibt. Auch die Integration des MouseProp-Algorithmus (siehe Abschnitt 3.4) hat darauf keine Auswirkungen. Implementiert ist dieser Ansatz unter PARIX und PVM.
Für das Online-Training (siehe Abschnitt 3.3.4) ist eine noch feinkörnigere Parallelisierung nötig, da bereits nach einem Musterpaar die Gewichte aktualisiert werden. Im Gegensatz zum vorherigen Ansatz sind nicht die zu berechnenden Aufgaben verteilt (domain decomposition), sondern jedes einzelne Problem wird parallel angegangen (function decomposition).
Die funktionalen Einheiten eines MP-Netzes sind die Neuronen. Sie gilt es zu verteilen. Von einer Partitionierung in "Querrichtung" ist abzuraten, da sie die Anzahl der einsetzbaren Prozessoren auf die Anzahl der Schichten begrenzt. Außerdem läßt sie aufgrund der hierarchischen Struktur eines MP-Netzes nur eine Verwendung des Batch-Trainings zu [14].
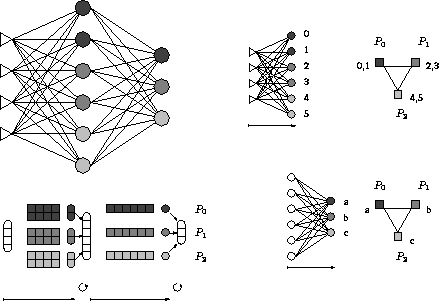
Abbildung 4.3: Parallele Forward-Phase
Die Partitionierung längs der Verbindungen erlaubt eine Parallelisierung des Online-Trainings. Für jede Schicht erhält jeder Prozessor die Zuständigkeit für einige Neuronen. Neben Schwellwert und Ausgabewert eines Neurons bekommt ein Prozessor auch die rezeptiven Gewichte zugewiesen.
Durch diese Aufteilung verringert sich der Speicherbedarf auf jedem Prozessor. Damit bietet sich die Möglichkeit, sehr große MP-Netze zu bearbeiten, die auf nur einem Prozessor nicht zu halten wären. Die Praxis zeigt jedoch, daß die Zeitkomplexität ein viel größeres Hindernis darstellt als die Speicherkomplexität. Schon das Training verhältnismäßig kleiner MP-Netze erweist sich als sehr zeitaufwendig.
In der Forward-Phase berechnet jeder Prozessor für seine Partition der jeweiligen Schicht die Ausgabewerte der ihm zugeteilten Neuronen (siehe Abbildung 4.3). Die dazu notwendigen rezeptiven Gewichte sind lokal vorhanden. Die Ausgabewerte der vorherigen Schicht sind jedem Prozessor bekannt. Damit erfolgt die Matrix-Vektor-Multiplikation sowie das Anwenden der Transferfunktion parallel. Das Resultat, also der Ausgabevektor der aktuellen Schicht liegt verteilt vor. Durch einen All-to-All-Broadcast [28] erhält jeder Prozessor die nicht von ihm berechneten Komponenten. Dieser Ausgabevektor wird für die im Anschluß stattfindenden Berechnungen der folgenden Schicht benötigt. Insgesamt ist also pro Schicht ein Broadcast erforderlich.
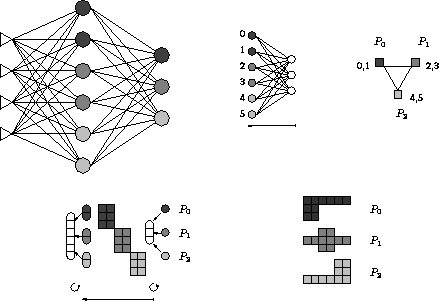
Abbildung 4.4: Parallele Backward-Phase nach YOON et al.
Die für die Fehlerberechnung in der Backward-Phase benötigten Gewichte entsprechen den Spalten der Gewichtematrix, lokal vorhanden sind aber nur die Zeilen. Um dennoch den Fehlervektor parallel berechnen zu können, werden in dem Ansatz von YOON et al. [28] neben den rezeptiven Gewichten auch die projektiven Gewichte eines Neurons gespeichert (siehe Abbildung 4.4). Die Berechnung der Fehlervektoren in der Backward-Phase verläuft ähnlich wie die der Ausgabevektoren in der Forward-Phase. Entsprechend der Zuständigkeit berechnet jeder Prozessor seinen Anteil. Durch einen All-to-All-Broadcast wird dieser zu einem auf jedem Prozessor identischen Vektor vervollständigt. Auch hier findet die Berechnung der Vektor-Matrix-Operation parallel statt.
Allerdings handelt man sich einen gewissen Overhead ein. Die projektiven Gewichte der verborgenen Neuronen müssen von dem jeweils zuständigen Prozessor aktualisiert werden. Dadurch verzögert sich die Backward-Phase. Trotz dieses Mehraufwands wurde die Idee von YOON et al. erfolgreich auf moderat parallelen Systemen umgesetzt [14].
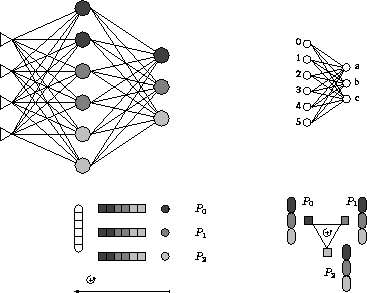
Abbildung 4.5: Parallele Backward-Phase nach MORGAN et al.
Einen anderen Weg, die Matrix-Vektor-Multiplikation zu parallelisieren, verfolgt die Idee von MORGAN et al. [11]. Statt die Spaltensumme zu berechnen, wird hier über die Zeilen aufaddiert. Jeder Prozessor bestimmt für alle Komponenten des Fehlervektors die Teilsumme aus den Produkten, die mit den vorhandenen Gewichten bestimmt werden können (siehe Abbildung 4.5).
Prozessor müßte für den Fehler von Neuron 0 und Neuron 1 folgende Summen berechnen:
Stattdessen berechnet den Vektor:
Entsprechende Vektoren berechnen die anderen Prozessoren. Die komponentenweise Addition der verteilten Vektoren gibt den korrekten Ergebnisvektor der Matrixmultiplikation. In einer All-to-All-Akkumulation, wie sie auch beim parallelen Batch-Training verwendet wird, tauschen die Prozessoren die Partialsummen untereinander aus und addieren sie dabei auf.
Die Integration des MouseProp-Algorithmus macht eine dynamische Lastverteilung erforderlich. Das zusätzliche Neuron bekommt der Prozessor, welcher die geringste Anzahl an verborgenen Neuronen der betreffenden Schicht besitzt.
Im folgenden Abschnitt werden die drei Parallelisierungsideen vor dem Hintergrund, daß die Informationen via Message-Passing ausgetauscht werden, verglichen. Die zeitlichen Kosten einer Kommunikation setzen sich aus einem relativ hohen konstanten Anteil und einem von dem zu verschickenden Volumen abhängigen Teil zusammen. Kommunikation bezeichnet in diesem Zusammenhang eine globale Operation, wie etwa All-to-All-Broadcast oder All-to-All-Akkumulation über alle Prozessoren.
Das Volumen einer Kommunikation bei der Parallelisierung des Online-Trainings bleibt für den Ansatz von MORGAN et al. konstant, während es bei YOON et al. mit zunehmender Prozessoranzahl sinkt. Das Kommunikationsvolumen bei der Parallelisierung des Batch-Trainings ist vergleichsweise groß, da statt Vektoren vom Ausmaß einer Schicht Daten im Umfang eines ganzen MP-Netzes verschickt werden. Allerdings bleibt das Volumen unbeeinflußt von der aufzuteilenden Problemgröße, also der Zahl der Trainingspaare. Dieses ergibt einen nahezu beliebig geringen Kommunikationsanteil an der Gesamtlaufzeit.
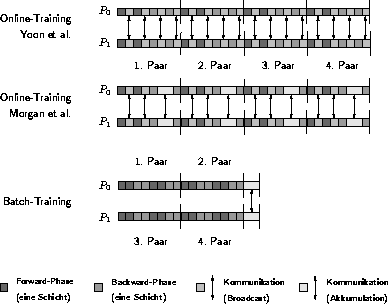
Abbildung 4.6: Kommunikation vs. Kalkulation
Die Anzahl der Kommunikationsaufrufe ist bei beiden Varianten des Online-Trainings gleich. Es ist ein Austausch unter allen Prozessoren nach dem Abarbeiten einer Schicht notwendig. Im Vergleich zum Batch-Training bedeutet dies eine vielfach höhere Kommunikationslast, da dort nur nach jeder Epoche kommuniziert wird. Abbildung 4.6 verdeutlicht dies für ein dreischichtiges MP-Netz mit einer verborgenen Schicht und einer relativ kleinen Trainingsmenge von vier Paaren, die auf zwei Prozessoren parallel abgearbeitet wird. Das Größenverhältnis der Blöcke zueinander ist willkürlich gewählt. Dennoch wird deutlich, daß sich das Batch-Training vor allem für große Trainingsmengen sehr effizient parallelisieren läßt.
Für die Parallelisierung des Online-Trainings zeigt sich eine sehr kleine Stückelung in Kommunikations- und Berechnungsphasen, die aufgrund der Randbedingungen des Backpropagation-Algorithmus nicht parallel zueinander ablaufen können. Auch die Berechnungsphasen selbst sind verhältnismäßig kurz. Zu kleine Häppchen machen die Parallelisierung unrentabel, weshalb sich das Online-Training erst für große MP-Netze mit einer entsprechenden Anzahl Neuronen lohnt.
Der hohe Kommunikationsanteil und auch die enge Verzahnung zwischen Kommunikation und Kalkulation haben zur Folge, daß die Parallelisierung des Online-Trainings nur auf solchen Architekturen Sinn macht, die über entsprechend leistungsstarke Kommunikationswege verfügen. Aus diesem Grund sind beide Ansätze des Online-Trainings auf Parallelrechnern unter PARIX (siehe Tabelle 4.1) implementiert worden.
PARIX [16] (PARallel extensions to UnIX) stellt dem Programmierer ein einheitliches Betriebssystem für alle Parallelrechner der Firma PARSYTEC zur Verfügung. Sowohl Transputer- als auch PowerPC-basierte MIMD-Rechner mit verteiltem Speicher können damit betreiben werden. Es bietet zum einen die volle Funktionalität eines UNIX-Betriebssystems, zum anderen eine optimale Unterstützung des Message-Passing durch die Parallelhardware.
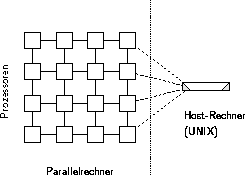
Abbildung 4.7: Ein Parallelrechner unter PARIX
Eine UNIX-Workstation, der Host-Rechner (siehe Abbildung 4.7) versorgt den Parallelrechner mit Programmcode und Daten. Ein-/Ausgabefunktionen können von beliebigen Prozessoren des Parallelrechners ausgeführt werden und lösen einen Remote Procedure Call auf dem Host-Rechner aus. Auf diese Art wird der Zugriff auf Dateisystem und Netzwerkkomponenten des Host-Rechners realisiert.
Die Prozessoren des Parallelrechners sind als zweidimensionales Gitter verschaltet, über das benachbarte Prozessoren miteinander kommunizieren. Diese Topologie wird standardmäßig von PARIX unterstützt. Darüberhinaus bietet PARIX die Möglichkeit, eine Verbindung zwischen zwei beliebigen Prozessoren zu etablieren (virtuelle Links). Das Routing eines virtuellen Links wird vom Betriebssystem verwaltet. Eine Menge virtueller Links kann zu einer virtuellen Topologie zusammengefaßt werden. Die geläufigsten Topologien (Pipe, Ring, Gitter, Baum, etc.) können durch Bibliotheksfunktionen erzeugt werden.
Eine parallele Applikation läuft auf einer rechteckigen Prozessorpartition, deren Ausmaße beim Programmstart angegeben werden. Alle Prozessoren der Applikation erhalten initial den gleichen Programmcode (SPMD-Modell). Jeder Prozessor kennt seine Gitterposition. Diese kann genutzt werden, um differenziert weiteren Programmcode nachzuladen (MIMD-Modell).
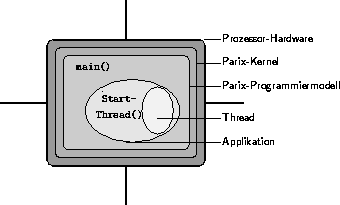
Abbildung 4.8: Threads unter PARIX
PARIX unterstützt sogenannte Threads. Hierbei handelt es sich um leichtgewichtige Prozesse, die im Kontext des erzeugenden Prozesses asynchron ablaufen. Ein Thread hat Zugriff auf alle globalen Variablen der Applikation und kann parallel zum Hauptprogramm eigenständig operieren. Threads stellen eine vergleichsweise günstige Resource dar, die häufig zur Abwicklung asynchroner Kommunikation eingesetzt wird. Zur Implementierung paralleler Programme steht sowohl ein ANSI-C als auch ein Fortran 77 Cross-Compiler einschließlich Bibliotheken für das jeweilige Zielsystem auf dem Host-Rechner zur Verfügung. Nur die Programmausführung selbst findet auf dem Parallelrechner statt. Für PARIX entwickelte Programme sind quelltextkompatibel, d.h. um ein Programm einer anderen als der bisherigen Architektur zugänglich zu machen, ist nur ein Übersetzungsvorgang notwendig.
| Rechner | Prozessortyp | MByte | Prozessoren/Knoten | Standort |
|---|---|---|---|---|
| MC-2 | T800 | 2 / 4 | 64 | Uni Osnabrück |
| GCel | T805 | 4 | 1024 | PC^2 Paderborn |
| PowerXplorer | MPC 601 | 8 | 4 | Uni Osnabrück |
| GC/PP | MPC 601 | 64 | 96 | PC^2 Paderborn |
Tabelle 4.1 zeigt eine Auflistung der Parallelrechner, für die unter PARIX mit einem parallelen Backpropagation-Algorithmus ein MP-Netz trainiert wurde. Die Rechner vom Typ GC sind am Paderborn Center for Parallel Computing ($\mbox{PC}^2$) beheimatet. Die PowerPC-basierten Systeme sind in Knoten organisiert, in denen jeweils ein T805 Transputer zur Kommunikation eingesetzt wird. Der GC/Power Plus verfügt in seiner jetzigen Ausbaustufe über 96 Knoten mit jeweils 2 MPC 601 Prozessoren.
Die parallele Implementation sowohl des Batch- als auch des Online-Trainings benutzen denselben Rahmen an Funktionen und Variablen. Durch das Betriebssystem bekommen alle Prozessoren die Parameter, mit denen das PARIX-Programm gestartet wurde. In einem ersten Schritt wird eine alle Prozessoren umspannende virtuelle Ringtopologie etabliert, auf der die Kommunikation stattfindet. Diese wird für eine gerade Anzahl Prozessoren in mindestens einer Richtung optimal auf die vorhandene Gittertopologie abgebildet (Abbildung 4.9). Die Ausführung von Ein-/Ausgabefunktionen findet nur auf einem Knoten statt. Dieser lädt alle relevanten Daten wie beispielsweise Netzgewichte oder Trainingsdaten und verteilt diese über den Ring. Eine Baumtopologie ist zwar besser geeignet, Daten zu verteilen, doch fällt diese Phase im Vergleich zur Trainingsdauer kaum ins Gewicht. Viel entscheidender ist eine Umsetzung der globalen Operationen All-to-All-Broadcast bzw. All-to-All-Akkumulation.
Jeder Prozessor hat zu Beginn des Trainings sowohl das komplette MP-Netz für das Batch-Training als auch sämtliche Trainingspaare für das Online-Training in seinem lokalen Speicher. Dieses erlaubt die gemeinsame Benutzung eines Großteils der Funktionen.
Für das Batch-Training berechnet jeder Prozessor seinen Ausschnitt der Trainings- und der Testmenge. Durch eine Akkumulation über alle Prozessoren werden nach einer deutlich kürzeren Epoche die Gewichtsänderungen angeglichen. Hierzu verschickt jeder Prozessor seine Änderungen für Schwellwerte und Gewichte zu seinem vorderen Nachbarn. Von seinem hinteren Nachbarn empfängt er dessen Änderungen. Diese schickt er im folgenden Schritt weiter nach vorne, addiert sie zu seinen Änderungen und empfängt die nächsten.
Für p Prozessoren erfordert die Akkumulation derartiger Kommunikationsschritte auf einer Ringtopologie. Auf einem zweidimensionalen Torus ließe sich diese Zahl auf reduzieren [13]. Doch ist eine Einbettung dieser Topologie in die Prozessortopologie in der Regel nicht ohne Kantendehnung möglich. Die dadurch entstehenden Verluste treiben die Kosten wieder in einen Bereich, den eine Ringkommunikation verursacht.

Abbildung 4.10: Kommunikation auf dem Ring
Um das Senden und Empfangen möglichst zügig zu bewerkstelligen, werden gleichzeitig zwei Kommunikationskanäle eines Prozessors bedient. Die PARIX-Funktion ASend() startet einen Thread, der im Hintergrund Daten zum Vordermann verschickt. Gleichzeitig empfängt das Hauptprogramm mittels Recv() Daten vom Hintermann. Die Benutzung der PARIX-Funktion Send() statt ASend() würde das Hauptprogramm blockieren bis sich ein Abnehmer für die Daten findet. Um keinen Deadlock zu provozieren, müßte dann in Schritten alternierend kommuniziert werden.
Das Recv() synchronisiert die Prozessoren und sorgt dafür, daß das nächste ASend() mit korrekten Daten aufgerufen wird. Ohne diese Synchronisation würde ASend() im schlimmsten Fall -mal den gleichen Vektor verschicken.
Der All-to-All-Broadcast beim Online-Training geschieht nach dem gleichen Prinzip, nur daß ein Prozessor eingehende Werte statt sie aufzuaddieren entsprechend der Partitionierung in seine lokalen Daten einsortiert. Da hierbei keine Fließkommaberechnungen anfallen, kann die gesamte Kommunikation ungestört und somit zügiger als die globale Akkumulation abgearbeitet werden.
Für die während und nach dem Training stattfindende Fehlerberechnung der Trainings- und Testmenge hat sich auch für das Online--Training eine Partionierung der Musterpaare als vorteilhaft erwiesen. Zwar ist hierfür ein Broadcast notwendig, um auf allen Prozessoren wieder identische Schwellwerte und Gewichte zu haben, doch entfällt abgesehen von der abschließenden Akkumulation des Fehlers weitere zeitraubende Kommunikation.
Die Integration des MouseProp-Algorithmus ist relativ problemlos. Die Berechnung der Oszillation eines Neurons kann parallel geschehen, die Prozessoren tauschen die Werte mit einem All-to-All-Broadcast untereinander aus. Die weitere Ermittlung eines aufzuspaltenden Neurons geschieht sequentiell. Der einfachste Weg, die Gewichte und Schwellwerte auf allen Prozessoren konsistent zu halten, besteht darin, mit einem Broadcast die MP--Netze anzugleichen, das Neuron aufzuspalten und für das quasi neue MP--Netz eine Lastverteilung zu ermitteln. Die im Anschluß stattfindende Bestimmung des sbic, erfordert die Berechnung der Fehlerwerte auf Trainings- und Testmenge. Der eigentlich dazu nötige Broadcast entfällt, da bereits für den Aufspaltungsvorgang die Gewichte und Schwellwerte ausgetauscht worden sind.
Nach Abschluß des Training werden noch einmal Schwellwerte und Gewichte angeglichen, um sie zum Beispiel über den I/O-Knoten in eine Datei zu schreiben.
Implementiert wurde der parallele Backpropagation-Algorithmus in ANSI-C unter PARIX in der Version 1.2 für reine Transputersysteme bzw. 1.3 für PowerPC-basierte Parallelrechner.
PVM (Parallel Virtual Machine) läßt ein heterogenes Netz von UNIX-Workstation und spezieller Parallelhardware als einen einzigen MIMD-Parallelrechner mit verteiltem Speicher erscheinen. Im Gegensatz zu PARIX handelt es sich bei PVM nicht um ein Betriebssystem, sondern um eine reine Laufzeitumgebung, die auf bestehenden Konzepten aufbaut. Unter UNIX-Workstations werden Daten via TCP/IP transferiert, auf Parallelrechnern werden dortige Message-Passing-Protokolle (zum Beispiel PARIX) benutzt (siehe Abbildung 4.11).
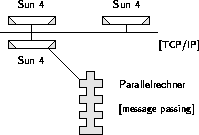
Abbildung 4.11: Virtueller Parallelrechner unter PVM
Das PVM-System besteht im wesentlichen aus zwei Teilen: Auf jedem beteiligten Rechnerknoten bearbeitet ein PVM-Daemon (pvmd) Anfragen von PVM-Applikationen (task). Diese Anfragen stammen von Funktionen der PVM-Bibliothek. Sie enthält alle Routinen, die zur Koorperation zwischen den Tasks einer Applikation nötig sind. Die Bibliothek unterstützt neben blockierender und nichtblockierender Task-zu-Task-Kommunikation auch Operationen auf Prozeßgruppen, wie Broadcasts und Synchronisationsbarrieren. Unterstützt werden die Programmiersprachen C, C++ und Fortran 77.
Eine Applikation besteht aus einer Menge von verteilten Tasks, die über ein Message-Passing-Protokoll kommunizieren. Tasks ebenso wie die beteiligten Rechner werden von PVM dynamisch verwaltet und können von der Applikation aus kontrolliert werden. Dieses erlaubt eine Programmierung im MIMD bzw. SPMD Modell. PVM kennt keine eigentliche Prozessortopologie, es sind beliebige Task-zu-Task Verbindungen möglich. Die Identifikation geschieht über eine eindeutige Task-ID (TID).
PVM ist für mehr als 50 Architekturen als Public Domain Software frei verfügbar. Dazu kommen noch mehrere kommerzielle Implementationen für Parallelrechner. Herausragender Vorteil der Formulierung paralleler Algorithmen mit PVM ist die Portabilität der Programme. Diese können komfortabel auf einem Workstation-Netz implementiert und getestet werden. Erst die eigentliche Anwendung benutzt eine parallele Architektur. Diese Portabilität hat natürlich gerade bei kommunikationsintensiven Algorithmen ihren Preis (siehe Abschnitt 4.5.2).
Unter PVM wurde eine parallele Variante des Batch-Trainings
implementiert. Um auch hier das SPMD-Konzept verfolgen zu können
wird das eigentliche Programm bp von einem anderen
PVM-Programm (mpil) aus gestartet. Dieses bekommt
neben dem auszuführenden Programm und dessen Argumenten
auch die Anzahl der Tasks, die durch die PVM-Funktion pvm_spawn()
gestartet werden. Das PVM-Laufzeitsystem verteilt
diese Tasks auf die beteiligten Rechner der virtuellen Maschine
(siehe Abbildung 4.12).
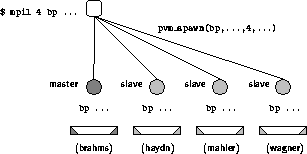
Abbildung 4.12: SPMD--Modell unter PVM
Die für die Kommunikation notwendigen Tasks-IDs empfangen die bp-Prozesse von ihrem Vater, der danach terminiert. Erst jetzt beginnt die eigentliche parallele Applikation. Analog zur Implementation unter PARIX wird eine Task bestimmt, die unter anderem die Dateioperationen erledigt. Über diese Master-Task läuft auch jegliche Kommunikation.
Alle bp Tasks werden Mitglied einer Gruppe. Sie dient zur Synchronisation der Prozesse. Die Master-Task verteilt Netzkonfiguration, Gewichte und Schwellwerte sowie Test- und Trainingsdaten. Nachdem jede Task die Größe ihrer Partition ermittelt hat, beginnt das Training. Nach Abarbeitung der lokalen Trainingsmenge findet eine All-to-All-Akkumulation der Gewichtsänderungen statt.
Da unter PVM jede Kommunikation a priori gleich teuer ist und auf einem Workstation-Verbund alle Rechner sich einen Kommunikationsweg teilen müssen, zielt die Realisierung der All-to-All-Akkumulation darauf ab, die globale Anzahl der Kommunikationen zu minimieren. Deshalb sammelt die Master-Task die Partialsummen auf, addiert sie zusammen und schickt das Ergebnis an die restlichen Tasks zurück (siehe Abbildung 4.13).
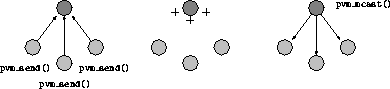
Abbildung 4.13: Globale Akkumulation unter PVM
Da nicht zwei Prozessoren gleichzeitig senden bzw. empfangen können, benötigt diese Operation für p Prozessoren einzelne Kommunikationsaufrufe. Virtuelle Topologien wie unter Parix sind nicht vorgesehen. Auf Workstation-Clustern machen sie auch keinen Sinn, da sie nicht die Kommunikationsleistung steigern.
Implementiert wurde das parallele Batch-Training unter PVM 3.3.7 auf einem Workstation-Cluster und unter PVM/PARIX, einer PVM 3.2 Implementation für Parallelrechner unter PARIX.
Der Speedup-Faktor s eines parallelen Rechners gibt an, wieviel mal schneller ein paralleler Algorithmus im Vergleich zum sequentiellen abgearbeitet werden kann:
Hierbei steht für die sequentielle Laufzeit auf einem Prozessor und für die Laufzeit des parallelen Programms auf p Prozessoren. Für Algorithmen, die keine Überlappung von Kommunikation und Berechnung zulassen, setzt sich die parallele Laufzeit folgendermaßen zusammen:
Da die Gesamtdauer der Kommunikationen in jeden Fall echt größer null ist, kann der Speedup nie den Wert p erreichen. Ein dem Speedup verwandtes Kriterium ist die Effizienz e, die ein parallels Programm erreicht:
In der Praxis sinkt für eine feste Problemgröße die Effizienz mit zunehmender Prozessoranzahl. Dies liegt zum einen daran, daß die Problemhappen eines Prozessors kleiner werden, zum andern aber die Zeit für die Kommunikation im besten Fall konstant bleibt, meistens eher steigt.
Die Trainingsdaten für das parallele Batch-Training stammen aus dem Verhulst-Prozeß (siehe Abbildung 3.10). Die Aufgabe entspricht der aus Abschnitt 3.5.2. Bei Präsentation der letzten drei Werte der Zeitreihe soll der zukünftige Wert prognostiziert werden. Trainiert wird ein MP-Netz mit 3 Eingabeneuronen, 6 Neuronen in der verborgenen Schicht und einem Ausgabeneuron. Die Zahl der zu trainierenden Paare beträgt 128, 1280 und 12800. Die Laufzeitmessungen wurden auf 3 Architekturen durchgeführt.
Ein Workstationverbund von Sun Sparc 10/20 kam unter PVM 3.3.7 zum Einsatz. Auf dem GCel und dem GC/PP (siehe Tabelle 4.1) wurde sowohl unter PARIX aus auch unter PVM trainiert. Der MC-2 und der PowerXplorer werden hier nicht betrachtet, da sie sich weitgehend nur bezüglich der Anzahl der Prozessoren von den anderen beiden Parallelrechnern unterscheiden.
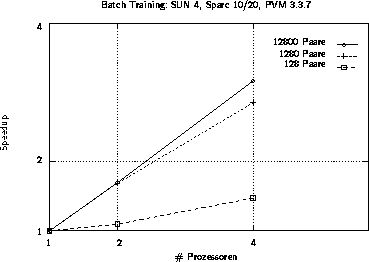
Abbildung 4.14: Speedups für das parallele Batch-Training auf einem Workstationverbund
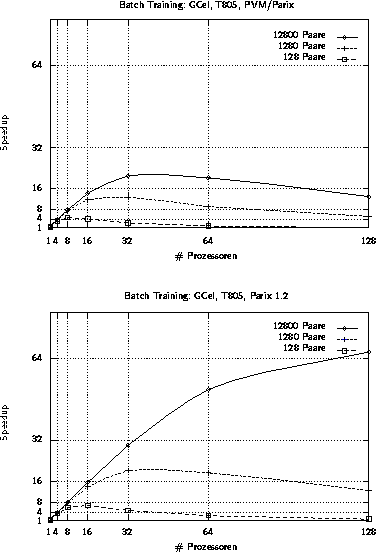
Abbildung 4.15: Speedups für das parallele Batch-Training auf dem GCel
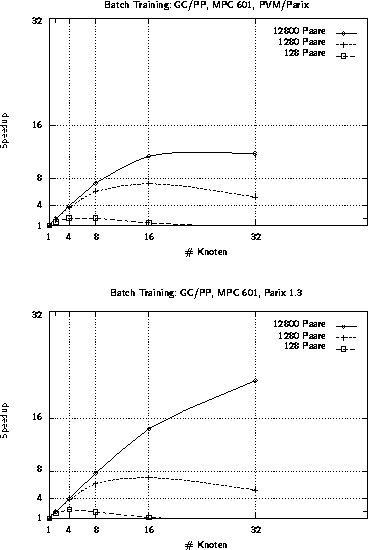
Abbildung 4.16: Speedups für das parallele Batch-Training auf dem GC/PP
Für vier Workstations zeigt sich eine moderate Beschleunigung des Trainings (siehe Abbildung 4.14). Wesentlich effektiver sind jedoch echte Parallelrechner. Auf dem GCel (siehe Abbildung 4.15) wird unter PARIX eine maximale Beschleunigung von knapp 67 auf 128 Prozessoren erreicht. Unter PVM knickt der Speedup-Graph sehr früh ab. Eine Ursache hierfür ist die mangelnde Unterstützung der lokalen Kommunikationsfähigkeiten, die unter PARIX ausgenutzt werden. Eine ähnliche Situation zeigt sich bei der letzten Architektur, dem GC/PP(siehe Abbildung 4.16). Auch hier läßt sich unter PARIX eine ganz passable Beschleunigung erreichen, während unter PVM der Speedup bereits bei 16 Knoten stagniert.
Für alle betrachteten Architekturen wird allerdings erst ab einer Problemgröße von mehr als 10000 Trainingsmustern ein respektabler Speedup erreicht. Weniger Trainingspaare sind bei einer großen Prozessoranzahl nicht rentabel.
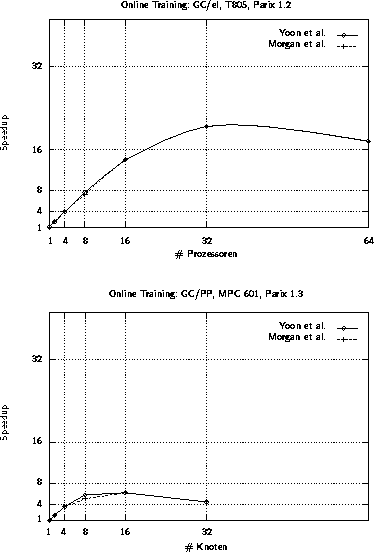
Abbildung 4.17: Speedups für das parallele Online-Training
Die Trainingsdaten für das parallele Online-Training kommen ebenfalls aus dem Umfeld der Zeitreihenprognose. Die trainierten Netze weisen 583 Eingabeneuronen, 256 verborgene Neuronen und ein Ausgabeneuron auf. Die Trainingsmenge besteht aus 20 Paaren. Die zugrundeliegende Zeitreihe beschreibt den Abverkauf eines Artikels in einem Supermarkt [22], [23]. Beide Varianten des parallelen Online-Trainings wurden unter PARIX auf dem GCel und dem GC/PP verwandt.
Abbildung 4.17 zeigt für jede Architektur den Speedup-Graphen beider Varianten. Für die gewählte Netztopologie zeichnen sich kaum Unterschiede zwischen der Idee von YOON et al. und der von MORGAN et al. ab. Auf dem GC-el wird immerhin noch ein Speedup von 20 auf 32 Prozessoren erzielt. Auf dem GC/PP wird bereits bei 16 Knoten die maximale Beschleunigung erreicht.
Für das parallele Batch Training ergeben sich gerade bei großen Trainingsmengen gute Beschleunigungswerte. Durch eine hinreichend große Anzahl an Trainingspaaren kann auch bei einer großen Prozessorzahl eine hohe Effizienz erzielt werden. Die für Kommunikation verwandte Zeit richtet sich allein nach der Größe der zu verschickenden MP--Netze und der Anzahl der Prozessoren. Dadurch kann ein günstiges Verhältnis zwischen Kommunikationsdauer und Rechenzeit erreicht werden.
Der Vergleich der Speedup-Graphen zeigt,
daß die Verwendung von PVM unter PARIX auf
Parallelrechnern nicht zu empfehlen ist, da
insbesondere bei großen Prozessorzahlen sehr viel
an Zeit durch Kommunikation verloren geht (siehe Abbildungen 4.15
und 4.16). Zwar enthält der PVM-Standard
einige globale Funktionen wie etwa pvm_gather(),
die hier verwendeten globalen Operationen müssen
jedoch unter PVM explizit formuliert werden.
Um portabel zu programmieren bietet sich stattdessen der
MPI-Standard [12] an. Zum Funktionsumfang von MPI
gehören kollektive Funktionen, die
bereits das bieten, was unter PVM nachgebildet werden muß.
Eine MPI-Implementation kann diese globalen Operationen
auf dem jeweiligen Zielsystem optimal unterbringen,
sodaß weniger Overhead entsteht.
Die Speedup-Graphen für das parallele Online-Training zeigen sowohl bei der Variante von YOON et al. als auch bei der von MORGAN et al. die Folgen des Kommunikationsaufwands. Die für diese Parallelisierung entscheidende Größe ist die Anzahl der Neuronen pro Schicht. Offensichtlich ist das zu verteilende Rechenpotential schon bei einer kleinen Anzahl Prozessoren erschöpft. Durch eine größere Anzahl verborgener Neuronen läßt sich eine höhere Effektivität erzielen. Eine Verbesserung bringt auch eine größere Anzahl von Ausgabeneuronen, doch ist diese durch die Problemstellung vorgegeben und dementsprechend schwieriger abzuändern als die Anzahl verborgener Neuronen.
Bei Problemen dieser Größenordnung zeigt sich kaum ein Unterschied zwischen den beiden Varianten. Der Vorteil einer zügigeren Kommunikation bei der Idee von YOON et al. geht zu Lasten eines erhöhten Rechenaufkommens, da einige Gewichtsänderungen doppelt auszuführen sind. Je höher die Anzahl verborgener Neuronen ist, desto mehr fallen diese Berechnungen ins Gewicht und kompensieren den ursprünglichen Vorteil.
Aufgrund der Rahmenbedingungen des Backpropagation-Algorithmus sind für alle Parallelisierungen globale Kommunikationen erforderlich. Die Kommunikationszeit wächst linear mit der Anzahl der Prozessoren, während die Berechnungsaufgaben im gleichen Maß schrumpfen. Der Speedup fällt dann wieder ab, wenn die globale Kommunikation eines Ergebnisses länger dauert als dessen Berechnung.
Transputer verfügen über eine für heutige Verhältnisse geringe Rechenleistung (1,5 MFLOPS), können aber verhältnismäßig schnell kommunizieren. PowerPC basierte Rechner verfügen über die gleiche Kommunikationsleistung bei vielfach höherer Verarbeitungsgeschwindigkeit (80 MFLOPS). Kommunikationen sind damit auf dem GC/PP relativ teuer, weshalb sich auf dem GCel bessere Beschleunigungen erreichen lassen.
Die Parallelisierung des Batch-Trainings erzielt unter PVM auf einem Workstation-Verbund gute Ergebnisse. Ausgezeichnete Resultate sind unter PARIX erreicht worden. Die Parallelisierung des Online-Trainings zeigt auf moderat parallelen Systemen eine ansprechende Beschleunigung. Insgesamt betrachtet, ist also durch die Parallelisierung des Backpropagation-Algorithmus die Trainingsdauer von MP-Netzen erheblich verkürzt worden.