Parallele Algorithmen

Oliver Vornberger, Fachbereich Mathematik/Informatik, Universität Osnabrück

ABSTRACT

Die zunehmende Verfügbarkeit von Multiprozessorsystemen hat das Interesse an geeigneter Anwendungssoftware steigen lassen. Hierbei zeigt es sich, daß der Entwurf und die Implementierung von parallelen Algorithmen für den traditionellen Programmierer bislang ungewohnte Konzepte verlangen.
In diesem Artikel sollen zunächst (in maschinenunabhängiger Weise) die gängigsten Parallelrechnerarchitekturen vorgestellt werden und anschließend die hierzu passende Programmierphilosophie anhand kleiner Beispiele erläutert werden.

           |            |            |
           |    SIMD    |    MIMD    |
           |  synchron  | asynchron  |
           |            |            |
-----------+------------+------------+
           |            |            |
 globaler  |    PRAM    |   C.mmp    |
 Speicher  |            |            |
           |            |            |
-----------+------------+------------+
           |            |            |
verteilter |    DAP     |    CM-5    |
 Speicher  |   MasPar   | Transputer |
           |    CM-2    |    iPSC    |
           |            |  Paragon   |
           |            |            |
-----------+------------+------------+

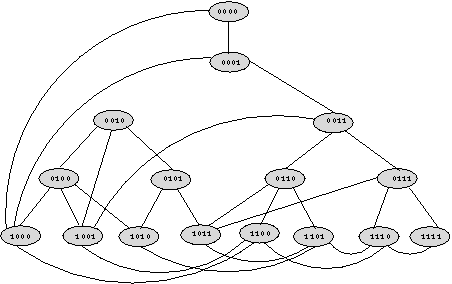
Abbildung 2: deBruijn-Netzwerk der Dimension 4

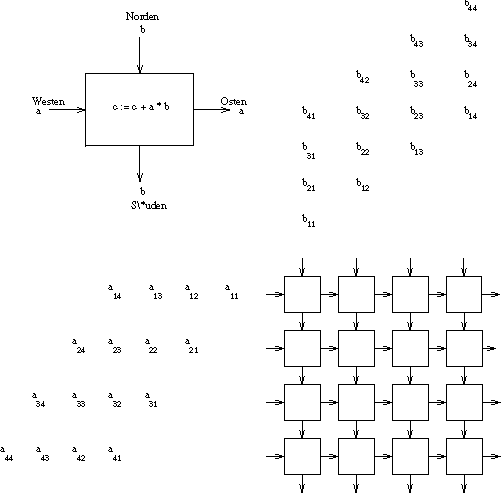
Abbildung 3: Matrixmultiplikation auf einem -Gitter

+-------------+--------------+   +--------------+-------------+
|             |              |   |              |             |
|@A sub {11}@ | @A sub {12}@ |   |@B sub {11}@  |@B sub {12}@ |
|             |              |   |              |             |
+-------------+--------------+   +--------------+-------------+
|             |              |   |              |             |
|@A sub {21}@ | @A sub {22}@ |   |@B sub {21}@  |@B sub {22}@ |
|             |              |   |              |             |
+-------------+--------------+   +--------------+-------------+

+--------------------------------------------------+---------------------------------------------------+
|                                                  |                                                   |
|@A sub {11}~~B sub {11}~+~A sub {12}~~B sub {21}@ | @A sub {11}~~B sub {12}~+~A sub {12}~~B sub {22}@ |
|                                                  |                                                   |
+--------------------------------------------------+---------------------------------------------------+
|                                                  |                                                   |
|@A sub {21}~~B sub {11}~+~A sub {22}~~B sub {21}@ | @A sub {21}~~B sub {12}~+~A sub {22}~~B sub {22}@ |
|                                                  |                                                   |
+--------------------------------------------------+---------------------------------------------------+

Initialisiere L mit einer Naeherungsloesung;
Initialisiere M mit dem Startproblem, in dem noch nichts fixiert ist;

REPEAT

  entferne t := billigstes Teilproblem aus M;
  expandiere t zu t1,    t2,    t3,  ...,   tk;
  berechne      u(t1), u(t2), u(t3), ..., u(tk);
  falls hierbei eine bessere Lösung als L entsteht, ersetze L;
  nimm von den expandierten die sinnvollen in die Menge M auf;
	
UNTIL Menge M enthält keine sinnvollen Teilprobleme mehr;

Falls ein Nachbar keine sinnvollen Teilprobleme mehr besitzt oder
falls ein Nachbar nur recht teure Teilprobleme hat, so versorge
ihn mit billigen Teilproblemen;

Falls L verbessert wurde, informiere die Nachbarprozessoren;

Abbildung 6: Lastverteilung für Branch-&-Bound

Motivation

Seit es Computer gibt, wurde von deren Anwendern der Wunsch nach mehr Rechenleistung laut. Insbesondere zur Simulation komplexer chemischer, physikalischer und biologischer Prozesse muß eine Unmenge von numerischen und symbolischen Operationen in einer vorgegebenen Zeitspanne durchlaufen werden. Man denke zum Beispiel an eine Wettervorhersage, die selbstverständlich vor dem zugehörigen Wetter berechnet sein sollte.

In den vergangenen Jahrzehnten konnte dieser Hunger nach Performance durch beeindruckende Verbesserungen im Bereich der Rechnerarchitektur gestillt werden: Etwa alle 5 Jahre wuchs die Anzahl der Instruktionen pro Zeiteinheit etwa um den Faktor 10. Die Supercomputer der neunziger Jahre bringen es inzwischen auf eine Peakleistung von über 100 Gigaflops.

Allerdings ist nun bald das Ende der Fahnenstange in Sicht, denn aufgrund von physikalischen Randbedingungen (wie z.B. der Lichtgeschwindigkeit) läßt sich die Taktfrequenz eines Mikroprozessors nicht mehr beliebig steigern. Dieser schlechten Nachricht stehen aber zwei gute gegenüber: Aufgrund von Massenfabrikation und standardisierten Herstellungsverfahren werden Hardwarekomponenten zunehmend billiger und kleiner. Was liegt also näher, als viele leistungsfähige Prozessorbausteine zu einer Einheit zusammenzuschließen und sie alle gemeinsam an einer Aufgabe arbeiten zu lassen?

Architektur

Zur Klassifikation solcher Multiprozessorsysteme zieht man ihren Kontrollmechanismus sowie ihre Speicherorganisation heran.

Beim Kontrollmechanismus unterscheidet man zwischen SIMD (single instruction, multiple data) und MIMD (multiple instruction, multiple data). SIMD bedeutet, daß unter zentraler Kontrolle ein einziges Programm auf allen Prozessoren (mit ggf. unterschiedlichen Daten) zum Einsatz kommt. Typischerweise werden dabei die einzelnen Instruktionen synchron abgearbeitet, was zur Folge hat, das sich alle Prozessoren jeweils an derselben Stelle im Code befinden, allerdings aufgrund ihrer individuellen Daten unterschiedliche Zustände aufweisen können. MIMD bedeutet, daß jeder Prozessor sein eigenes Programm in asynchroner Weise auf seine eigenen Daten ansetzt. Dies hat zur Folge, daß sich zu jedem Zeitpunkt alle Prozessoren an unterschiedlichen Stellen ihres Codes befinden können, der allerdings durchaus durch Übersetzung desselben Programm-Source entstanden sein kann.

Bei der Speicherorganisation unterscheidet man zwischen global memory und distributed memory. Global memory verlangt Hardware-Unterstützung für Speicherzugriffe aller Prozessoren auf einen gemeinsamen Adreßraum. Die Synchronisation zwischen den Rechenpartnern erfolgt dann durch Manipulation gemeinsam bekannter Objekte, d.h., ein von Prozessor geschriebenes Datum kann unmittelbar von Prozessor gelesen werden. Distributed memory bedeutet eine Partitionierung des Adreßraums, so daß jeder Prozessor seinen nur ihm zugänglichen Lokalspeicher verwaltet. Die Synchronisation erfolgt dann durch das Austauschen von Nachrichten zwischen den Rechenpartnern, wobei das Kommunikationsmedium ein globaler Bus sein kann oder ein Netzwerk mit Punkt-zu-Punkt-Verbindungen.

Abbildung 1 zeigt die aus Kontrollmechanismus und Speicherorganisation resultierenden Architekturvarianten zusammen mit einigen typischen Vertretern.

Das SIMD -Konzept wird oft zur Formulierung von Algorithmen herangezogen, bei denen die Prozessorzahl von der Problemgröße abhängt, z.B. dürfen Prozessoren Daten bearbeiten. Diesem theoretischen Ansatz mit recht eleganten Algorithmen steht eine konstante Prozessorzahl beim MIMD -Ansatz gegebenüber, der sich insbesondere in der distributed memory-Variante als universelle Plattform für parallele Algorithmen durchzusetzen scheint.

Topologie

Eine wichtige Rolle bei den distributed memory-Maschinen spielt die Struktur des benutzten Verbindungsnetzwerks. Formal läßt es sich als ein ungerichteter Graph beschreiben, dessen Knoten den Prozessoren und dessen Kanten den direkten Kommunikationsverbindungen entsprechen. Zur Beurteilung einer Topologie werden folgende Aspekte herangezogen:

• Läßt sich die Struktur auch für große Knotenanzahl realisieren? Bausteine mit variablem Verzweigungsgrad sind technologisch ungünstig.
• Wie wächst der Durchmesser (d.h. das Maximum der kürzesten Wege zwischen allen Paaren) mit der Anzahl der Knoten? Kleine Durchmesser reduzieren den Kommunikationsoverhead, da Nachrichten zwischen nicht unmittelbar benachbarten Prozessoren bereits nach wenigen Schritten am Ziel sind.
• Wie läßt sich das Routing (d.h. das Finden eines Verbindungswegs für eine weiterzureichende Nachricht) formulieren? Der Routing-Algorithmus hat großen Einfluß auf die Vermeidung von Kommunikations-Deadlocks.
• Existiert ein Hamiltonkreis, d.h. eine Rundreise über alle Netzwerkknoten ohne Wiederholung? Hierdurch lassen sich zahlreiche Routinen zur Detektion gewisser Programmzustände, z.B. Terminierung, einfacher formulieren.

Sehr verbreitet aufgrund ihrer technologischen Handhabbarkeit sind das lineare Array und das zwei- oder dreidimensionale Gitter. Diese Topologien haben einen konstanten Knotengrad, erlauben einfaches Routing und sind für zahlreiche Problemstellungen, insbesondere numerischer Natur mit Matrix-artigen Operationen, geeignet.

Verlangt die Problemstellung einen kleineren Durchmesser, so bietet sich oft der Hypercube an: Eine Kante zwischen zwei Prozessoren existiert genau dann, wenn sich die Dualzahldarstellungen ihrer Kennungen an genau einer Stelle unterscheiden. Dieses Konzept ist in einfacher Weise skalierbar, da sich ein Hypercube der Dimension aus zwei Hypercubes der Dimension zusammensetzt. Bei Prozessoren entsteht ein Verzweigungsgrad von (denn an so vielen Bits kann die Dualzahldarstellung differieren), und auch der Durchmesser beträgt : Beginnend bei einer beliebigen Startadresse routet man systematisch zu einer gegebenen Zieladresse, indem jeweils der Prozessor angelaufen wird, der das nächste Bit aus dem Zielpattern in seiner Kennung trägt. Durch Induktion über die Dimensionszahl läßt sich leicht die Hamilton-Eigenschaft nachweisen.

Der Schwachpunkt variabler Verzweigungsgrad kann ausgebügelt werden, wenn man zu einem leicht aufwendigeren Routing bereit ist. Bei deBruijn-Graphen hat ein Knoten mit der Adresse die Nachfolger und . Auf diese Weise entsteht ein gerichteter Graph mit Ausgangsgrad . Ignoriert man die Richtungen, so ist jeder Knoten mit höchstens vier Nachbarn verbunden, siehe Abbildung 2. Dies ist besonders geeignet für Transputersysteme, die pro Prozessor genau vier Kommunikationslinks aufweisen. Trotz des konstanten Verzweigungsgrads beträgt der Durchmesser nur , da eine beliebige Zieladresse angesteuert werden kann, indem jeweils durch einen Knotenübergang das vorderste Bit der momentanen Adresse entfernt und das nächste im Zielpattern benötigte Bit an die momentane Adresse gehängt wird. Die Existenz von Hamiltonkreisen ergibt sich durch Anwendung eines Satzes über Euler-Graphen.

Performance

Zur Beurteilung von Parallelen Algorithmen dient in erster Linie der Speedup, das Verhältnis von Sequentialzeit zur Multiprozessorzeit. Genauer: Sei die Zeit, die der beste bekannte Algorithmus zur Lösung der Probleminstanz auf einem Mono-Prozessor benötigt, und sei die Zeit, der der parallele Algorithmus zur Lösung auf Prozessoren benötigt, dann beträgt der Speedup für diese Instanz

• .
  

Die Effizienz für Instanz berücksichtigt den Material-Aufwand zur Erreichung des Speedups:

• .
  

Schließlich definiert man als Maß für den Gesamtaufwand die Kosten

• .
  

Ist die Verteilung der Instanzen bekannt, läßt sich der durchschnittliche Speedup angeben als gemittelter Speedup über alle möglichen Probleminstanzen. Als Idealvorstellung wird im Mittel ein fast linearer Speedup erhofft, aufgrund unterschiedlicher Programmabläufe im sequentiellen bzw. parallelen Fall kann für einzelne Instanzen der Speedup durchaus superlinear sein.

Um ein Gefühl für die Vielfalt der Programmiermethoden im Bereich der parallelen Algorihmen zu vermitteln, sollen im folgenden anhand von beispielhaften Problemstellungen die parallelen Lösungsprinzipien für die oben zitierten Architekturklassen vorgestellt werden.

SIMD & Global Memory

Als Vertreter der SIMD -Klasse mit globalem Speicher fungiert die Parallel Random Access Machine, kurz PRAM . Dieses oft zitierte, nie gebaute Modell läßt sich weiter klassifizieren nach der Freiheit beim Zugriff auf den gemeinsamen Speicher:

• EREW (exclusive read, exclusive write),
• CREW (concurrent read, exclusive write),
• ERCW (exclusive read, concurrent write),
• CRCW (concurrent read, concurrent write).

Sicherlich läßt sich gleichzeitiges Lesen technologisch realisieren, beim gemeinsamen Schreiben wollen wir jedoch voraussetzen, daß alle beteiligten Prozessoren jeweils identische Werte schreiben, wenn sie dieselbe Zelle referieren. Hierdurch ergibt sich in natürlicher Weise eine eindeutige Semantik der Operation.

Unter dieser Voraussetzung und unter der Annahme, daß eine varibale Anzahl von Prozessoren zur Verfügung steht, betrachten wir nun das Problem, aus einer Folge von Zahlen das Maximum zu bestimmen. Wir nehmen der Einfachheit halber an, alle Zahlen seien verschieden. Zum Einsatz kommen Prozessoren, bezeichnet mit , die alle Zugriff auf das globale

a : array[1..n] OF INTEGER

haben.

Zunächst wird die globale Variable

sieger : array[1..n] OF BOOLEAN

initialisiert mit TRUE, d.h.

FOR ALL 1<=i<=n DO parallel
   P1i:  sieger[i]:=TRUE
END;

Damit wird jeder Zahl bescheinigt, daß sie (vorläufig) als größte gilt.

Nun vergleichen alle Prozessoren gleichzeitig die ihnen zugewiesenen Zahlenpaare:

FOR ALL 1<=i,j<=n DO parallel
   Pij:  IF a[i]<a[j]
         THEN sieger[i]:=FALSE
         END
END;

Offenbar scheiden nun im direkten ``Zweikampf'' solche Zahlen aus dem Rennen aus, zu denen es eine größere Zahl gibt. Bei manchen wird die Tatsache, daß sie ``verloren'' haben, gleich mehrfach festgestellt. Man beachte aber, daß alle Prozessoren, die gleichzeitig auf die Komponente

sieger[i]

zugreifen, dort denselben Wert, nämlich FALSE, einspeichern.

Zum Schluß wollen wir noch den Sieger ermitteln, d.h. die größte Zahl der Variablen max zuweisen:

FOR ALL 1<=i<=n DO parallel
   P1i:  IF sieger[i]
         THEN max:=a[i]
         END
END;

Die Laufzeit des Verfahrens ist konstant (je ein Schritt für Initialisierung, Vergleich, Auswertung) bei Prozessoren. Da der beste sequentielle Algorithmus Schritte benötigt, beträgt der Speedup , die Effizienz 1/ und die Kosten . Somit strebt die Wirtschaftlichkeit dieses verblüffend einfachen Verfahrens mit wachsender Problemgröße gegen , was nicht verwundert, da wir mit quadratischem Materialeinsatz nur eine lineare Beschleunigung erzielt haben.

SIMD & Distributed Memory

Wie auch bereits in der SIMD -Variante mit globalem Speicher soll im nächsten Beispiel der verwendete Prozessor eine sehr elementare Aufgabe ausführen, d.h., er fungiert als sehr kleines Rädchen in einem sehr großen Getriebe, bestehend aus einem synchron getakteten Netzwerk. Die zu lösende Aufgabe besteht in der Multiplikation zweier Matrizen. Als Topologie wählen wir dazu ein 2-dimensionales Gitter mit Prozessoren, deren Verbindungen zu ihren vier Nachbarn wir mit Norden, Osten, Süden, Westen bezeichnen. Die Arbeitsweise eines einzelnen Prozessors besteht darin, die von Norden und Westen hereinkommenden Daten zu multiplizieren, dieses Produkt einer lokal gehaltenen Summe hinzuzuaddieren und dann den westlichen Wert nach Osten und den nördlichen Wert nach Süden weiterzuschieben (siehe Abbildung 3). Zu Beginn werden alle lokalen Summen mit initialisiert und sodann die beiden zu multiplizierenden Matrizen und schrittweise von Westen bzw. von Norden in das Netzwerk eingespeist. Damit die jeweils zueinander gehörenden Faktoren eines Produkts zum richtigen Zeitpunkt aufeinander treffen, wird das Einlesen der Zeilen von bzw. Spalten von um jeweils eine Zeiteinheit versetzt gestartet. Nachdem Matrix komplett von Westen nach Osten und Matrix komplett von Norden nach Süden das Gitter durchlaufen haben, liegt das Produkt verteilt im Netzwerk vor. Genauer gesagt befindet sich im Speicher von Prozessor der Term

und kann nun ohne weitere Modifikation durch Weiterschieben nach Osten das Netzwerk als Ausgabe verlassen.

Der Aufwand pro Produktbildung in jedem Prozessor ist konstant, der längste Weg eines Datums besteht, aufgrund des zeitversetzten Einlesens, aus Schritten. Da alle diese Wege parallel zueinander beschritten werden, resultiert eine Gesamtzeit von bei Prozessoren. Verglichen mit dem traditionellen Algorithmus zur Matrixmultiplikation verursacht dies einen Speedup von und eine Effizienz von . Somit wird hier eine optimale Wirtschaftlichkeit erreicht, die daher rührt, daß die Gesamtzahl der erforderlichen arithmetischen Operationen ohne Wartezeit und ohne Redundanz auf die beteiligten Prozessoren gleichmäßig verteilt werden konnten.

MIMD & Global Memory

Beide SIMD -Varianten erlaubten recht kurze algorithmische Formulierungen, da die Anzahl der Prozessoren in Abhängigkeit von der Menge der Input-Daten so gewählt werden konnte, daß für jede elementare Teilaufgabe ein eigens zugewiesener Prozessor zur Verfügung stand. Somit entfällt das bei MIMD -Rechnern typischerweise vorhandene Problem, einen variabel großen Input auf eine konstant dimensionierte Hardware zu verteilen. Diese Aufgabe, genannt Mapping, wird jedoch wesentlich erleichert, wenn wir Maschinenmodelle mit globalem Speicher betrachten, da wir ohne Berücksichtigung der Zugriffskosten jedem Prozessor erlauben, beliebige Teile der Eingabedaten zu referieren. Um dies zu verdeutlichen, wollen wir das Problem der Matrixmultiplikation erneut aufgreifen, diesmal jedoch nur vier Prozessoren bereitstellen.

Wie Abbildung 4 zeigt, ist jeder Prozessor zuständig für die Berechnung eines Viertels der Ergebnismatrix . Hierzu betrachten wir die beiden Eingabe-Matrizen und als Zusammenfassungen von jeweils vier Teilmatrizen. Aufgrund der Dekompositionseigenschaft des Matrixprodukts können diese Substrukturen nun von den zuständigen Prozessoren abgerufen werden. Z.B. benötigt Prozessor , der die linke obere Teilmatrix von bestimmt, die beiden oberen Teilmatrizen von sowie die beiden linken Teilmatrizen von . Zählen wir der Einfachheit halber nur die Anzahl der durchgeführten Elementarmultiplikationen, so entstehen für jeden Prozessor durch die zweimalige Verknüpfung zweier Matrizen ein Aufwand von . Bezogen auf die sequentielle Schrittzahl bedeutet dies ein Speedup von und eine Effizienz von . Derselbe Ansatz läßt sich für jede Zahl von Prozessoren durchführen, durch die sich die Zahl ganzzahlig teilen läßt. Man beachte, daß beim Zugriff auf und gleichzeitiges Lesen gewisser Teilbereiche erfolgt, jedoch beim Erstellen von exclusives Schreiben für jede Teilmatrix garantiert ist.

MIMD & Distributed Memory

Die algorithmisch interessanteste Klasse liegt zweifelsohne vor, wenn eine konstante Anzahl von asynchron arbeitenden Prozessoren mit lokalem Speicher verschaltet ist. Die typischen Probleme beim Entwurf eines parallelen Algorithmus für diese Konfiguration lassen sich wie folgt charakterisieren:

• Topologie

Abhängig von der Problemstruktur muß ein Kommunikationsgraph für die Prozessoren gewählt werden. Hierbei ist man je nach verwendeter Hardware auf ein fest vorgegebenes Verschaltungsmuster angewiesen (z.B. 2-dimensionales Gitter) oder kann ggf. die Nachbarschaftsbeziehungen noch frei konfigurieren (z.B. gemäß deBruijn, falls ein kleiner Durchmesser von Belang ist).

• Mapping

Hierunter versteht man eine kostengünstige Einbettung des Prozeßgraphen in den Prozessorgraphen. Der Prozeßgraph repräsentiert durch seine Knoten einzelne Tasks des Lösungsverfahrens (gewichtet durch die zu erwartende Rechenlast) und durch seine Kanten eine eventuell erforderliche Nachbarschaft zwischen den Tasks (gewichtet durch den zu erwartenden Kommunikationsbedarf). Kostengünstig heißt, daß nach Möglichkeit die Rechenlast gleichmäßig den beteiligten Prozessoren zugewiesen wird und solche Prozesse, die unmittelbaren Kommunikationsbedarf angemeldet haben, nach Möglichkeit auf dieselben oder auf nah benachbarte Prozessoren abgebildet werden.

• Lastverteilung

Durch das Mapping wird bereits eine statische Lastverteilung definiert, die zu Beginn der Rechnung eine Unter- oder Überbeschäftigung der Prozessoren verhindert. Je nach gewähltem Lösungsansatz kann es jedoch erforderlich sein, während der Rechnung einen dynamischen Lastausgleich durchzuführen. Hierzu ist parallel zur Rechnung fortwährend ein Maß für die pro Prozessor anliegende unerledigte Arbeit auszuwerten und ggf. durch Austausch von Teilaufgaben die ``Schieflage'' zu korrigieren.

Um diese Konzepte näher zu erläutern, wählen wir ein Beispiel aus dem Bereich Operations Research, nämlich das Lösen eines kombinatorischen Optimierungsproblems. Formal wird dabei ein ganzzahliger Vektor gesucht, der gewissen Randbedingungen genügt und dabei eine Zielfunktion minimiert. Sind keine strukturellen oder mathematischen Zusatzinformationen vorhanden, muß zur Beantwortung dieser Frage ein gigantischer Lösungsraum durchsucht werden, wobei zur Beschleunigung gewisse Teilräume ausgegrenzt werden können, sofern durch geeignete Heuristiken ihre Suboptimalität nachgewiesen wird. Diese Technik, bekannt als Branch-&-Bound, verwaltet eine Menge von sogenannten Teilproblemen, in denen bereits einige der gesuchten Lösungsvariablen fixiert sind. In einem Branch-Schritt, auch genannt Expansion, werden anhand einer weiteren Lösungsvariablen alle zulässigen Verlängerungen generiert. Schließlich läßt sich in effizienter Weise für ein Teilproblem eine untere Schranke bestimmen, die angibt, wie teuer jede Gesamtlösung mindestes wird, welche als Bestandteil die Fixierungen von enthält.

Beispielsweise könnte für das Traveling Salesman-Problem (billigste Rundreise durch ein System von Städten ohne Wiederholung) das Expandieren darin bestehen, daß eine Teiltour an ihrer letzten Stadt zu all jenen Städten erweitert wird, die durch eine direkte Verbindung erreichbar sind und nicht bereits auf dieser Teiltour besucht wurden. In die untere Schranke bezieht man oft die (sehr schnell zu berechnenden) Kosten eines Minimum Spanning Tree ein, der über die noch nicht besuchte Menge von Städten gespannt wird. Der prinzipielle Ablauf wird in Abbildung 5 skizziert.

Hierbei wird ein Teilproblem als sinnvoll bezeichnet, falls seine Schranke kleiner als der Wert der bisher billigsten Lösung ist. Somit enthält nach Beenden der Schleife die optimale Lösung.

Je nach Qualität der verwendeten unteren Schranke entsteht eine enorme Anzahl von gleichzeitig abzuspeichernden Teilproblemen sowie eine daraus resultierende lange Laufzeit. Somit bietet sich eine Parallelisierung auf einem System von vernetzten Prozessoren an, die in ihren Lokalspeichern jeweils disjunkte Teile der Menge verwalten. Genauer: Ein ausgezeichneter Prozessor, der Master, initialisiert seine Menge mit dem Startproblem, alle anderen Rechner, die Slaves, beginnen mit einer leeren Menge. Alle durchlaufen den oben beschriebenen sequentiellen Algorithmus, allerdings führt nun das Leerlaufen der Menge nicht zum Abbruch, sondern zur Kontaktaufnahme mit einem Nachbarprozessor zwecks Arbeitsbeschaffung.

An dieser Stelle ist nun eine dynamische Lastverteilung angebracht. Um die Kernidee des sequentiellen Branch-&-Bound, das jeweils billigste Teilproblem zu expandieren, aufrechtzuerhalten, muß jeder Prozessor bemüht sein, an dem im Netzwerk global billigsten Teilproblem zu arbeiten. Somit muß in die REPEAT-Schleife eine Kommunikationsroutine eingebaut werden, die bei Arbeitslosigkeit oder bei einer Schieflage bzgl. der Teilproblemkosten für ein Verschieben der Arbeitslast sorgt. Außerdem sollten neue obere Schranken schnellstens verbreitet werden. Abbildung 6 skizziert das unregelmäßig stattfindende Austauschen von Nachrichten.

Auf diese Art und Weise simuliert das verteilte System den sequentiellen Algorithmus, indem die Menge partitioniert in den jeweiligen Lokalspeichern gehalten wird und an mehreren, jeweils möglichst billigen, Teilproblemen gleichzeitig expandiert wird.

Damit ein zügiges Durchmischen der Arbeitshäppchen und ein unverzügliches Weiterreichen neuer oberer Schranken sichergestellt ist, sollte eine Topologie mit kleinem Durchmesser gewählt werden. Bei frei konfigurierbaren Systemen mit Knotengrad bietet sich das deBruijn-Netzwerk an.

Terminierung

Zum Schluß soll noch das Problem der Terminierung angesprochen werden, welches im sequentiellen Fall trivialerweise durch eine Meldung des einzigen Prozessors mitgeteilt werden kann. In einem asynchron arbeitenden Multiprozessorsystem liegt folgende Situation vor: Es gibt aktive und passive Prozesse. Aktive Prozesse haben im Augenblick noch mehrere unerledigte Tasks in ihrer Work-Queue, können also nach einer Weile, wenn die Arbeit erledigt ist, spontan passiv werden. Passive Prozesse sind zur Zeit arbeitslos, können aber durch den Empfang einer Nachricht wieder mit Arbeit versorgt werden und wechseln dann in den Zustand aktiv. Die entscheidende Frage lautet: Wann sind alle Prozesse passiv?

Zur Lösung dieser Aufgabe wird der Hamiltonkreis genutzt, der als Teilgraph in der gewählten Prozessortopologie enthalten sein sollte. Sobald der Master zum ersten Mal passiv wird, schickt er ein grünes Token auf die Reise. Längs des Hamiltonkreises wird das Token von passiven Prozessen weitergereicht. Bei Erhalt des grünen Tokens beim Master färbt dieser es rot und schickt es erneut in die Runde. Ein rotes Token wird von einem passiven Prozeß rot weitergereicht, falls er seit dem letzten Tokendurchgang keine neue Arbeit erhalten hat, andernfalls wird es grün weitergereicht. Erhält der Master ein rotes Token, so folgert er, daß alle Prozesse passiv sind.

• Und wenn sie nicht
  gestorben sind, dann
  leben sie noch heute!