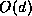is linear to the search depth 
.
Depth-First Search (DFS) first expands the initial state by generating all successors to the root node. At each subsequent step, one of the most recently generated nodes is taken and its successors are generated. (The successors may be sorted according to some heuristic prior to expansion.) If at any instance, there are no successors to a node, or if it can be determined that this node does not lead to a solution, the search backtracks, that is, the expansion proceeds with one other of the most recently generated nodes.
DFS is usually implemented with a stack holding all nodes (and immediate successors)
on the path to the currently explored node.
The resulting space complexity of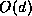
is linear to the search depth .
Backtracking is the simplest form of DFS. It terminates as soon as a solution is found. Therefore, optimality cannot be guaranteed. Moreover, backtracking might not terminate in graphs containing cycles or in trees with unbounded depth.
Depth-First Branch-and-Bound (DFBB) uses a heuristic function to eliminate parts of the search space that cannot contain an optimal solution. It continues after finding a first solution until the search space is exhausted. Whenever a better solution is found, the current solution path and value are updated. Subtrees that are known to be inferior to the current solution are cut off.
Best-First Search sorts the sequence of node expansions
according to a heuristic function.
The popular A* algorithm [11][9] uses a heuristic
evaluation function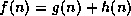 
to decide which successor node 
to
expand next.
Here, 
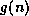is the measured cost of the path from the initial state to the
current node and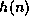 
is the estimated completion cost
to a nearest goal state.
If 
does not overestimate the remaining cost,
A* is said to be admissible, that is, it finds an optimal (least cost)
solution path.
Moreover, it does so with minimal node expansions [11];
no other search algorithm (with the same heuristic ) can do better.
This is possible, because A* keeps the search graph in memory
and performs a best-first search on the gathered node information.
One disadvantage of A* is its exponential space complexity of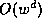 
in trees of width 
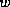and depth .
The high demands on
storage space makes it infeasible for many applications.
Iterative-Deepening A* (IDA*) [6]
simulates A*'s best-first node expansion by a
series of depth-first searches, each with the cost-bound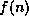 
increased by the minimal amount.
The cost-bound is initially set to the heuristic estimate of the root node.
Then, for each iteration, the bound is increased to the minimum value
that exceeded the previous bound until a solution is found.
Like A*, IDA* is admissible (finds an optimal solution)
when does not overestimate the solution cost [6].
But it does so with a much lower space complexity of .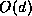
At first sight, it might seem that IDA* wastes computing time by repeatedly re-examining the same nodes of the shallower tree levels. But theoretical analyses [8][6] give evidence that IDA* has the same asymptotic branching factor as A* when the search space grows exponential with the search depth.