Einleitung
Next: Modifizierte Backpropagation-Lernregel
Up: Parallele Backpropagation
Previous: Parallele Backpropagation
Neuronale Netze haben sich als geeignet erwiesen, nicht offensichtliche
Zusammenhänge komplexer Systeme bis hin zum deterministischen Chaos
vergleichsweise gut zu adaptieren und zu verallgemeinern.
Prinzipiell können Neuronale Netze beliebige Abbildungen
nach einer gewissen Trainingsphase approximieren.
Insbesondere bei der Analyse und Vorhersage von Zeitreihen
sind Neuronale Netze eine Alternative zu den klassischen Verfahren.
So werden Neuronale Netze bereits heute zur Bedarfsberechnung
z.B. für Fernwärme oder elektrischen Strom sowie zur Bestimmung
volkswirtschaftlicher Kenngrößen kommerziell eingesetzt [1], [2], [3].
Neuronale Netze lernen durch Präsentation diskreter Funktionswerte,
eine den Werten zugrundeliegende Abbildung zu approximieren.
Bei der Vorhersage von Zeitreihen lernt das Netz anhand von Werten aus der Vergangenheit,
dem sogenannten Trainingsset.
Bei Eingabe von  aufeinanderfolgenden Werten soll der Wert zum Zeitpunkt
aufeinanderfolgenden Werten soll der Wert zum Zeitpunkt 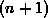 als Ergebnis der Abbildung in der Output-Schicht erscheinen.
Es wird solange die komplette Trainingsmenge gelernt,
bis der Abbildungsfehler unter eine gewisse Schranke gesunken ist.
Ein solcher Durchgang wird als Epoche bezeichnet.
Zur Vorhersage kann das so trainierte Netz eingesetzt werden,
indem die letzten
als Ergebnis der Abbildung in der Output-Schicht erscheinen.
Es wird solange die komplette Trainingsmenge gelernt,
bis der Abbildungsfehler unter eine gewisse Schranke gesunken ist.
Ein solcher Durchgang wird als Epoche bezeichnet.
Zur Vorhersage kann das so trainierte Netz eingesetzt werden,
indem die letzten  bekannten Werte eingegeben werden
und das Netz den Wert für
bekannten Werte eingegeben werden
und das Netz den Wert für 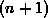 bestimmt.
bestimmt.
Ein zur Prognose häufig gewählter Ansatz ist das
Feedforward Multilayer Perceptron (FMP)
Netzwerk mit der Backpropagation-Lernregel [4].
Das Trainieren dieses Netzwerktyps erfordert einen hohen Rechenzeitaufwand,
der sich mit einer effizienten Parallelisierung des Lernvorgangs signifikant
verringern läßt.
Frank M. Thiesing
Mon Dec 19 15:35:21 MET 1994
 aufeinanderfolgenden Werten soll der Wert zum Zeitpunkt
aufeinanderfolgenden Werten soll der Wert zum Zeitpunkt 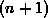 als Ergebnis der Abbildung in der Output-Schicht erscheinen.
Es wird solange die komplette Trainingsmenge gelernt,
bis der Abbildungsfehler unter eine gewisse Schranke gesunken ist.
Ein solcher Durchgang wird als Epoche bezeichnet.
Zur Vorhersage kann das so trainierte Netz eingesetzt werden,
indem die letzten
als Ergebnis der Abbildung in der Output-Schicht erscheinen.
Es wird solange die komplette Trainingsmenge gelernt,
bis der Abbildungsfehler unter eine gewisse Schranke gesunken ist.
Ein solcher Durchgang wird als Epoche bezeichnet.
Zur Vorhersage kann das so trainierte Netz eingesetzt werden,
indem die letzten  bekannten Werte eingegeben werden
und das Netz den Wert für
bekannten Werte eingegeben werden
und das Netz den Wert für 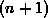 bestimmt.
bestimmt.