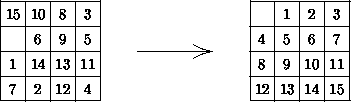
Figure 1: Das 4
4- bzw. 15-Puzzle in einer beliebigen Ausgangsstellung (links)
und in der Zielstellung (rechts)
Die iterative Tiefensuche findet Anwendungen in der Operations Research und in der Künstlichen Intelligenz. Dieses Verfahren kann etwa für zweidimensionale Pack-Probleme (Cutting-Stock Problem) [14] oder im Bereich des VLSI-Chip-Entwurfs (Floorplan-Area-Optimization) [15] angewendet werden.
Typische Anwendungen der iterativen Tiefensuche zeichnen sich durch die folgenden Eigenschaften aus:
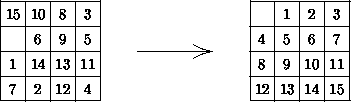
Figure 1: Das 44- bzw. 15-Puzzle in einer beliebigen Ausgangsstellung (links)
und in der Zielstellung (rechts)
Eine einfache Anwendung mit den oben genannten Eigenschaften ist das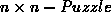 
[8].
Das nn -Puzzle besteht aus einem festen Rahmen der Größe nn, in dem
sich n
-1 durchnumerierte Spielsteine befinden,
ein Feld ist leer.
In einem Zug kann nun ein zum leeren Feld benachbarter Spielstein auf dieses Feld
verschoben werden.
Die Lösung des nn-Puzzles besteht darin, eine beliebige Ausgangsstellung mit
einer minimalen Anzahl von Zügen in eine definierte Zielstellung zu überführen.
Das nn-Puzzle ist ein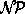 
-vollständiges Problem [9].
Der Algorithmus IDA* ist das bislang einzige Verfahren, welches kleinere Instanzen, wie
etwa das 44-Puzzle mit annehmbaren Ressourcen lösen kann.
Dabei werden bei 100 zufälligen Instanzen im Durchschnitt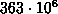 
Knoten
betrachtet [4].
Als Heuristik wird die Manhattan-Distanz verwendet, welche sich aus der
Summe der kürzesten Distanzen aller Steine von ihren Zielpositionen
berechnet.
Während der Fehler dieser Heuristik im Falle des 44-Puzzles noch relativ
gering ausfällt, hat sich diese Heuristik zur Lösung des 45-Puzzles als
nicht sehr geeignet erwiesen, da die sich ergebenden Suchbäume trotz der Verwendung
einer Heuristik noch sehr großsind [13].
So wurden bei der Lösung einer zufälligen Instanz dieses Problems mehr als
1.5 Billionen Knoten expandiert.