Künstliche Neuronale Netze haben eine Reihe erfolgreicher Anwendungen in der Industrie gefunden. In diesem Artikel soll ihr Einsatz für die Prognose von Zeitreihen vorgestellt werden. Am Beispiel von Verkaufszahlen wird dargestellt, wie Neuronale Netze vorhersagen können, was die Zukunft bringt.
Neuronale Netze sind informationsverarbeitende Systeme, die aus einer großen Anzahl einfacher Einheiten bestehen. Diese sogenannten Neuronen sind durch gerichtete Verbindungen miteinander zu Netzwerken verbunden. Über diese senden sich die Neuronen Information in Form ihrer Aktivierung zu.
Neuronale Netze weisen eine grobe Analogie zum Gehirn auf, in dem die Informationsverarbeitung durch sehr viele Nervenzellen stattfindet, die im Vergleich zum Gesamtsystem sehr einfach sind und die den Grad ihrer Erregung über Nervenfasern an andere Nervenzellen weiterleiten.
Neben dieser Motivation durch die teilweise Ähnlichkeit zu erfolgreichen biologischen Systemen beziehen künstliche Neuronale Netze aber auch einen großen Teil ihrer Motivation aus der Tatsache, daß es sich hierbei um massiv parallele, lernfähige Systeme handelt, die auch für sich genommen interessant sind. Diese Algorithmen sind in Form von Programmen, Netzwerksimulatoren oder auch in Form spezieller neuronaler Hardware in vielen Anwendungsgebieten einsetzbar [1,2].
Das wesentliche Element dieser künstlichen Neuronalen Netze ist ihre Lernfähigkeit. Diese Fähigkeit, ein Klassifikationsproblem selbständig aus Trainingsbeispielen zu lernen, ohne daß es dazu explizit programmiert werden muß, machen Neuronale Netze universell einsetzbar.
Die Anwendung Neuronaler Netze ist einfach; trotzdem sind sie aufgrund ihrer nicht-linearen Struktur in der Lage, auch komplexe verborgene Strukturen zu erkennen.
Seit in den 40-er Jahren die ersten künstlichen Neuronalen Netze entworfen wurden, ist die Anzahl von untersuchten Modellen von Jahr zu Jahr gestiegen. Für verschiedene Anwendungen werden unterschiedliche Netzmodelle eingesetzt: Das Neuronale Netz gibt es nicht. Die Modelle unterscheiden sich erheblich voneinander, sowohl in der Funktionalität des einzelnen Neurons als auch in ihrer Verbindungsstruktur [3,4]. Zu den Grundlagen Neuronaler Netze sei hier auf den Artikel von V. Sperschneider verwiesen [5], der einen Überblick liefert.
Im folgenden werden ausschließlich Netze vom erfolgreichen Typ Feedforward Multilayer Perceptron verwendet. Diese sind lernfähige Klassifikatoren, die durch Präsentation von Trainingsdaten die funktionalen Zusammenhänge zwischen Input- und Outputmustern erlernen können, ohne daß ihnen in irgendeiner Art und Weise die unbekannten analytischen Abhängigkeiten eingegeben worden sind.
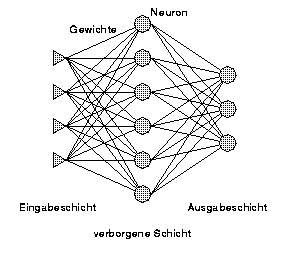
Ein Neuronales Netz besteht aus Neuronen und gewichteten Kanten, die diese verbinden. Beim Feedforward Multilayer Perceptron (MLP) sind die Neuronen in Layers strukturiert, und jedes Neuron eines Layers ist mit allen Neuronen der beiden benachbarten Layer verbunden, mit zwei Ausnahmen: Das Input-Layer hat keine Vorgänger, und das Output-Layer hat keine Nachfolger. Die Schichten zwischen Input- und Output-Layer werden Hidden-Layer (verdeckte Schichten) genannt. Die Anzahl der Hidden-Layer variiert, ist aber selten größer als zwei (s. Abbildung 1).

Abbildung 1: Feedforward Multilayer Perceptron
Ein Neuron wird durch seine Vorgänger aktiviert und gibt seine Ausgabe an alle seine Nachfolger weiter. Dadurch ergibt sich ein Informationsfluß von der Input- zur Output-Schicht. Dabei sind alle Neuronen mit Ausnahme der Input-Schicht aktiv. Die Neuronen der Input-Schicht reichen einen angelegten Eingabewert lediglich durch.
Jedes aktive Neuron im Multilayer Perceptron berechnet die gewichtete Summe der Ausgaben seiner Vorgänger. Zur Berechnung der Aktivierung eines Neurons gehört außerdem die Addition eines Neuron-eigenen Schwellwertes betaj. Diese Aktivierung wird mit Hilfe einer Transferfunktion f in die Ausgabe des Neurons überführt. Bei vier Vorgängern (siehe Abbildung 2):
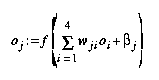
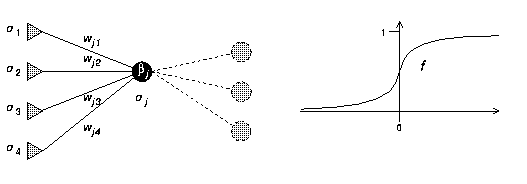
Abbildung 2: Arbeitsweise eines Neurons im Perceptron
Als Transferfunktion wird häufig eine Sigmoide verwendet, die den Wertebereich auf ]0,1[ beschränkt.
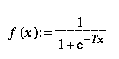
In einem Netz können die Gewichte wji und die Schwellwerte betaj geändert und damit verschiedene Funktionen konstruiert werden.
Die typische Anwendung eines Multilayer Perceptrons ist die Approximation einer unbekannten und analytisch schwer faßbaren Abbildungsvorschrift f. Von dieser mehrdimensionalen Abbildung sind einige Argumente x und die zugehörigen Funktionswerte y bekannt: f(x) = y. Das Ziel ist es, daß das Neuronale Netz die Abbildungsvorschrift anhand der exemplarischen Werte erlernt und dadurch in der Lage ist, den Funktionsverlauf zu generalisieren, so daß auch ein nicht trainiertes x auf ein sinnvolles y abgebildet wird.
Dazu kann das MLP als Blackbox betrachtet werden, das sich durch Präsentation der Argumente in der Input-Schicht und der Werte in der Output-Schicht selbständig trainiert.
Der Lernalgorithmus für MLP-Netze wurde Mitte der 80er Jahre von Rumelhart et al. vorgestellt und hat sich zu einem Standard entwickelt [6]. Beim Training werden durch den Backpropagation-Algorithmus während der mehrmaligen Präsentation aller Trainingspaare die Netzgewichte automatisch so eingestellt, daß der Abbildungsfehler minimiert wird.
Initial sind die Schwellwerte der Neuronen und die Gewichte mit Zufallswerten besetzt. Wird ein Input-Vektor x angelegt, wird gemäß der Arbeitsweise der einzelnen Neuronen im MLP in der sogenannten Vorwärtsphase ein Output-Vektor y* ermittelt. Dieser weicht i.a. vom vorgegebenen Sollwert y ab.
Damit das MLP die Abbildungsvorschrift f(x) = y erlernen kann, wird für jedes Trainingspaar (x, y) in der Vorwärtsphase ein y* mit einem Fehler delta = y - y* ermittelt. Dieser Fehler wird nun in der Rückwärtsphase des Trainings zurückpropagiert, von der Output-Schicht in Richtung Input-Schicht (s. Abbildung 3).
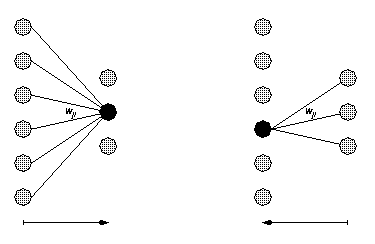
Abbildung 3: Vorwärts- und Rückwärtsphase des Backpropagation-Algorithmus
Dabei werden in den Hidden-Schichten jeweils wieder Fehler berechnet und nach vorne weitergegeben. Mit Hilfe dieser Fehler wird eine Korrektur der Netzgewichte und Schwellwerte vorgenommen.
Bei der Art der Fehlerminimierung handelt es sich um ein Gradientenabstiegsverfahren, daß den mittleren quadratischen Fehler minimiert. Die Geschwindigkeit des Verfahrens wird durch einen Parameter eingestellt, der als Lernrate bezeichnet wird.
Durch das mehrmalige Training aller Trainingspaare wird der Abbildungsfehler in ein lokales Minimum geführt. Durch die Verwendung eines Momentumterms, der den Gradienten in Richtung des vorhergehenden ablenkt, können solche lokalen Minima verlassen werden in der Hoffnung, ein besseres Minimum mit kleinerem Fehler zu finden.
Die Prognose von Zeitreihen spielt insbesondere im wirtschaftlichen Bereich eine große Rolle. Sowohl bei Aktien- und Börsenkursen als auch beim Verbrauch von Strom und Fernwärme versuchen Analysten, aus dem Verlauf der regelmäßig anfallenden Daten die zukünftige Entwicklung vorherzusagen, um fundierte Entscheidungen treffen zu können. Hierzu werden neuerdings zunehmend Neuronale Netze eingesetzt [7,8].
Beispielsweise haben wir ein System entwickelt, das es ermöglicht, Prognosen des wöchentlichen Abverkaufs von Artikeln eines Supermarkts vorzunehmen, um so die Disposition zu unterstützen und die Lagerhaltungskosten zu minimieren. Dazu werden Neuronale Netze eingesetzt, das scheinbar chaotische Käuferverhalten anhand der Vergangenheitsentwicklung zu erlernen. Viele Faktoren haben Einfluß auf das Käuferverhalten. Deshalb ist die Auswahl der richtigen Einflußfaktoren und deren Modellierung entscheidend. Die realen Daten stammen aus den Scannerkassen eines Supermarkts.
Für die Zeitreihenprognose werden die MLP-Netze darauf trainiert, den Verlauf der Zeitreihe zu approximieren und für die Prognose zu generalisieren. Der Vorteil des Einsatzes Neuronaler Netze liegt in ihrer Fähigkeit, sich ändernden Rahmenbedingungen schnell anpassen zu können und durch zusätzliches Lernen die Prognosequalität selbständig zu verbessern.
Zur Prognose einer Zeitreihe mit einem MLP wird ein gleitendes Zeitfenster mit n Vergangenheitswerten über die Zeitreihe gelegt. Die Trainingsaufgabe besteht darin, aus n Werten in der Input-Schicht auf den nächsten Wert zu schließen. Das Training erfolgt anhand der bekannten Werte. Das trainierte Netz wird zur Prognose eingesetzt, indem die letzten n bekannten Werte in der Input-Schicht angelegt werden, die das Netz auf den Prognosewert abbildet (s. Abbildung 4).
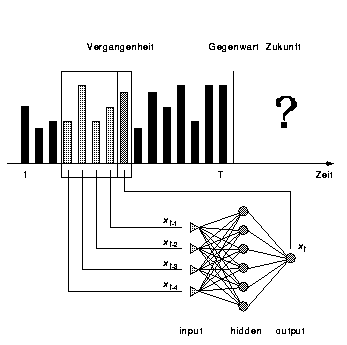
Abbildung 4: Zeitreihenprognose mit MLP
Diese Art des Vorgehens ermöglicht es lediglich, anhand der zeitlichen Entwicklung dieser einen Zeitreihe deren Zukunft zu prognostizieren, sozusagen aus sich selbst heraus. Häufig sind es aber äußere Einflüsse, die den Verlauf einer Zeitreihe beeinflussen. Diese Einflußfaktoren müssen ebenfalls in Form einer Zeitreihe vorliegen und werden über zusätzliche Neuronen in die Inputschicht des MLP eingegeben. Zu den erklärenden Einflüssen zählen insbesondere solche, die für den zu prognostizieren Zeitpunkt t schon bekannt sind.
Wir wollen in der vorgestellten Anwendung den Abverkauf von Artikeln in einem Supermarkt prognostizieren. Die Daten über die Anzahl der verkauften Artikel und deren Preise liegen wochenweise vor. Der Abverkauf der betrachteten Produkte ist starken Schwankungen ausgesetzt, die auf teils bekannte, teils unbekannte Einflußfaktoren zurückzuführen sind. Entscheidende Auswirkungen auf das Käuferverhalten haben offenbar Werbeaktionen, Preisveränderungen und Feiertage. Deshalb werden die Daten über die Art und Dauer von Werbekampagnen und Preisveränderungen ebenfalls in die Prognose mit einbezogen. Auch die Zahl der Öffnungstage in einer Woche wird berücksichtigt.
Die wöchentlichen Abverkaufszahlen und der Preis eines exemplarischen Artikels sind in Abbildung 5 zusammen mit den Aktions- und Feiertagen dargestellt.
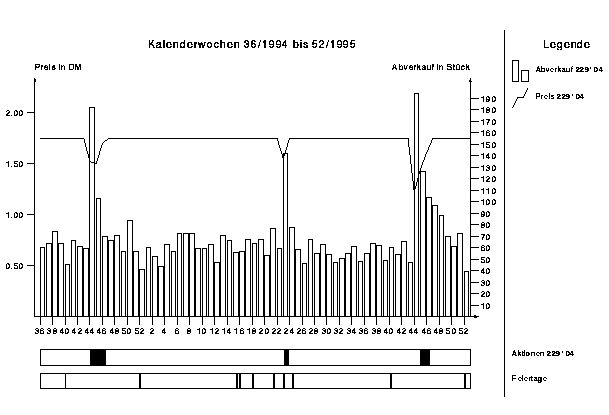
Abbildung 5: Abverkauf, Preis, Aktionen von Artikel 229104, Feiertage
Gut zu erkennen ist der starke Absatzanstieg, der mit einer Sonderpreisaktion einhergeht. Ziel der Prognose ist es insbesondere, solche Ausreißer im Verkauf bei der Disposition vorherzusehen, um ausreichende Lagerbestände zu haben. Dazu wird das Neuronale Netz auf genau diese Zusammenhänge zwischen Preis, Aktionen und Absatz trainiert.
Entscheidend hierbei ist, daß die Informationen über Preis, Aktionen und Feiertage für die nähere Zukunft bereits vorliegen und in die Prognose einfließen können.
Eine effiziente Vorverarbeitung der anfallenden Daten ist notwendig, um sie dem MLP eingeben zu können. Insbesondere sollte aufgrund der gewählten Sigmoidfunktion eine Skalierung der unterschiedlichen Inputwerte auf das Intervall ]0, 1[ erfolgen. Dies ist auch notwendig, um die qualitativen und quantitativen Einflußgrößen gleichgewichtig zu machen.
Bei der Vorverarbeitung von Zeitreihendaten werden neben der notwendigen Normierung noch weitere Techniken angewandt. So kann es z.B. sinnvoll sein, die Werte vorher zu logarithmieren. Insbesondere bei Zeitreihen, die ein ständiges Wachstum aufweisen, ist zur Beseitigung dieses Trends das Differenzieren der Werte notwendig. Dadurch besteht die abgeleitete Zeitreihe dann aus den Differenzen aufeinanderfolgender Werte.
Im Beispiel der Prognose von Abverkäufen sind die relevanten Verkaufsinformationen als wöchentliche Daten gegeben. Der Abverkauf ist nur bis einschließlich Woche T-1 bekannt, die anderen Zeitreihen auch darüber hinaus. Die verwendeten Rohdaten eines Artikels in einer Woche t sind:
Die Normierung erfolgt auf das Intervall [0.1,0.9], da die Werte 0 und 1 von der Sigmoide nicht angenommen werden.
Der Abverkauf in Woche t, SALt, wird linear mit Hilfe seines Maximums normiert:
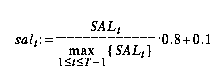
Auch die Anzahl der Aktions- bzw. Feiertage im Verhältnis zu sechs Wochentagen wird linear normiert. Die Preisveränderung wird nur qualitativ und nicht quantitativ erfaßt. Das Inputneuron für den Preis in Woche t, prit, hat den Wert
Für jede vergangene und deshalb bekannte Woche t wird ein Vektor der Werte der normierten Zeitreihen verwendet:
vect := (holt , advt , prit , salt)
Für eine Woche t ``in der Zukunft'', für die ja gerade der Abverkauf trainiert bzw. vorhergesagt werden soll, fließen lediglich die Einflußfaktoren ein:
{vect} hat := (holt , advt , prit)
Als Inputvektor des MLP werden die bekannten Daten aus einem Zeitfenster von n Wochen, vect-n bis vect-1, verwandt sowie die Einflußfaktoren für die Wochen t und t+1. Das MLP wird darauf trainiert, diesen Input auf den normierten Wert des Abverkaufs, salt+1, abzubilden. Die Abbildung 6 stellt Input und Output schematisch dar.
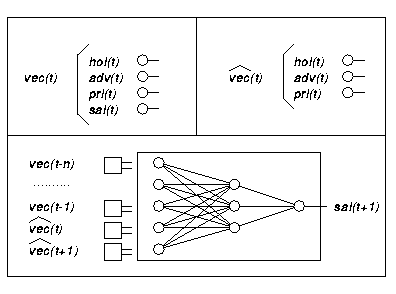
Abbildung 6: Input für MLP
Aus praktischen Gründen wird in Woche T mit den bekannten Abverkäufen bis einschließlich Woche T-1 die Prognose für die Woche T+1 bestimmt, damit genug Zeit für die Diposition bleibt.
Dazu wird das trainierte Netz in Woche T mit den Daten der n vergangenen Wochen und den Einflußfaktoren der aktuellen und kommenden Woche abgefragt. Als Ausgabewert wird der Wert salT+1 erwartet, der zurücktransformiert werden muß zum Wert für den prognostizierten Abverkauf des Artikels in der Woche T+1.
Die Herausforderung beim Einsatz Neuronaler Netze ist die Einstellung der richtigen Parameter: Die Anzahl der verdeckten Schichten, die Anzahl der Neuronen in diesen und die Lernrate sind nur einige Variablen, die vom Entwickler so eingestellt werden müssen, daß zufriedenstellende Prognose-Ergebnisse erreicht werden. Besonderes Augenmerk muß dabei zuvor auf die Vergangenheitstiefe und die Auswahl der Einflußfaktoren sowie deren Modellierung gelegt werden, bevor das Neuronale Netz vorhersagen kann, was die Zukunft bringt. Die Optimierung all dieser Parameter bringt viele Testläufe mit sich.
Am Beispiel des Artikels 229104, der im betrachteten Zeitraum 3 Aktionen aufweist (s. Abbildung 5), soll das Ergebnis der Prognose den echten Daten gegenübergestellt werden.
Das ausgewählte MLP-Netz hat neben einer Eingabeschicht zwei aktive Schichten. Die verdeckte Schicht hat 15 Neuronen, und die Ausgabeschicht besteht aus einem Neuron. Die 22 Inputneuronen ergeben sich wie folgt: Bei einer Vergangenheitstiefe von n=4 Wochen ergeben sich jeweils 6 Neuronen für Preisveränderungen, Aktionsinformationen und Feiertage. Diese Daten sind bis einschließlich der Prognosewoche bekannt.
Unbekannt ist dagegen natürlich der zu prognostizierende Abverkauf für die letzten beiden Wochen. Deshalb werden 4 Neuronen für diese Zeitreihe benötigt.
Abbildung 5 zeigt die Abverkaufsinformationen des Artikels 229104. Abbildung 7 zeigt gegenübergestellt den tatsächlich eingetretenen Abverkauf sowie die sukzessive erstellten Prognosen mit dem Neuronalen Netz ab Woche 17/95.
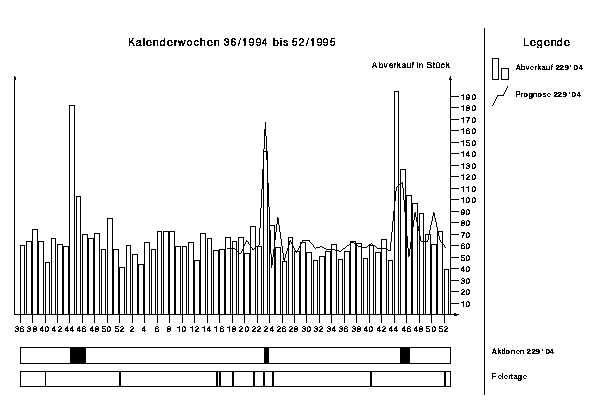
Abbildung 7: Abverkauf und Prognose für Artikel 229104
Besonders auffällig ist die Fähigkeit des neuronalen Netzes, bei den beiden Aktionen den stark ansteigenden Abverkauf vorherzusagen. Das Käuferverhalten bei einer Aktion wurde anhand der vorangegangenen Aktionen erlernt. Auch wenn die Höhe des Abverkaufs bei einer Aktion unterschiedlich stark ansteigt, so wird doch qualitativ die richtige Tendenz vom Netz prognostiziert.
Neuronale Netze sind lernfähige Klassifikatoren, die insbesondere in nicht-linearen, chaotischen Systemen selbsttätig die analytisch nicht bekannten Zusammenhänge zwischen Ein- und Ausgabemuster erlernen, um nach dem Training mit unbekannten Daten abgefragt zu werden. Dabei ist keine Identität zwischen gelehrtem und angefragtem Muster erforderlich, sondern es genügt eine Ähnlichkeit der aktuellen Daten mit den Trainingsdaten. Diese Eigenschaft der Neuronalen Netze zur Generalisierung macht sie so interessant für den Einsatz zur Klassifikation und Prognose von unscharfen und verrauschten Daten.