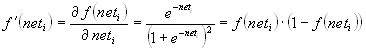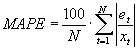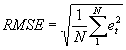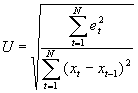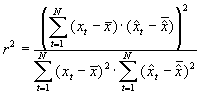- Methoden der Datenanalyse und -prognose
- Mathematische Verfahren
- Multiple Regressionsanalyse
Die multiple Regressionsanalyse ist ein einfaches und weit verbreitetes Verfahren, um die Abhängigkeiten von exogenen und endogenen Variablen zu modellieren. Dabei ist man nicht zwangsläufig auf die lineare Regression beschränkt, in der Praxis spielt diese jedoch die wichtigste Rolle. Im folgenden wird das Verfahren kurz dargestellt.
Funktionsweise
Will man den Zusammenhang einer abhängigen (endogenen) Variable y von k unabhängigen (exogenen) Variablen xi (i = 1, 2, ..., k) modellieren, nimmt man an, y lasse sich als gewichtete Summe der einzelnen exogenen Variablen ausdrücken. Für diese xi existieren N Realisierungen xti (t = 1, 2, ..., N). Im linearen Fall erhält man so:
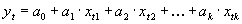
Man beachte, daß die xti auch zeitlich geshiftete exogene Zeitreihen darstellen können. Die Gewichte ai (i = 0, 1, ..., k) werden in aller Regel nach der Methode der kleinsten Abweichungsquadrate bestimmt. Mit dieser Methode lassen sich die Gewichte mathematisch exakt bestimmen. Für die praktische Anwendung wurden SAS (insbesondere die Statistik-Prozedur "Reg") sowie GAUSS und MS Excel 97 verwandt, die jedoch alle auf numerische Verfahren zurückgreifen.
Die Koeffizienten der Regressionsgleichung können allerdings nur dann zuverlässig bestimmt werden, wenn die betrachtete Zeitreihe schwach stationär ist. Man spricht von der schwachen Stationarität einer Zeitreihe, wenn die Mittelwerte und Varianzen zweier ausreichend großer Teilmengen yt...yT und yt+k...yT+k für alle k gleich, also zeitlich invariant sind. Ist die schwache Stationarität nicht gegeben, so wird der Differenzenfilter 1. Ordnung der Form
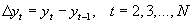
so oft angewandt, bis die Stationarität vorliegt.
Bei der (multiplen) Regressionsanalyse treten verschiedene Probleme auf, die bei der Bewertung der Ergebnisse beachtet werden müssen:
- Um die Regressionsanalyse optimal einzusetzen, muß bereits im Vorfeld klar sein, welcher Art die Zusammenhänge zwischen exogenen und endogenen Variablen sind. Dabei ist Linearität oftmals nicht gegeben und lineare Verfahren eignen sich in diesen Fällen dementsprechend schlecht zur Modellierung.
- Ausreißer werden bei Bestimmung der Gewichte ai zu stark bewertet, da hier die quadratische Abweichung minimiert wird. So haben 100 Werte mit Abweichungen d den gleichen Einfluß wie ein Wert mit Abweichung 10×
d. Gegebenenfalls ist hier also eine Vorverarbeitung angebracht.
Klassisches Komponentenmodell
Das klassische Komponentenmodell ist als eine Erweiterung der Regressionsanalyse zu verstehen, die diese um weitere, i.a. nichtlineare Terme erweitert.
Funktionsweise
Man nimmt an, daß eine Zeitreihe aus verschiedenen Komponenten zusammengesetzt ist, die den tatsächlichen Verlauf der Zeitreihe ergeben. Das klassische Komponentenmodell unterscheidet drei Komponenten:
- Der Trend, der eine langfristige systematische zeitliche Entwicklung des mittleren Niveaus darstellt. Er wird meist durch eine Gerade dargestellt.
- Die zyklische Komponente, die eine (jahres-) zeitlich relativ unverändert auftretende Schwankung der Werte modelliert. Eine typische zyklische Schwankung ist die Saisonkomponente, die in manchen Darstellungen des Komponentenmodells als gesonderte Komponente behandelt wird.
- Die Zufalls- oder Restkomponente, die nicht erklärbare Abweichungen beinhaltet. Da die beiden anderen Komponenten durch mathematische Funktionen dargestellt werden und die betrachtete Zeitreihe als Realisierung eines statistischen Prozesses noch zufallsgestört ist, muß angenommen werden, daß die Kombination aus Trend und zyklischer Komponente die Zeitreihe nicht vollständig erklären.
Es lassen sich nun aus diesen Annahmen unterschiedliche Modelle erstellen, die sich in der Art der Verknüpfung der Komponenten unterscheiden. Die zwei bedeutendsten sind das additive Modell und das multiplikative Modell. Meist wird angenommen, daß sich die Komponenten additiv überlagern. So erhält man eine formale Beschreibung des additiven Modells:
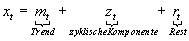
Vielfach tritt auch der Fall ein, daß mit dem mittleren Niveau auch die Streuung um dieses Niveau zunimmt. In diesem Fall findet das multiplikative Modell Verwendung:
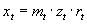
Im folgenden sollen nun gängige Verfahren vorgestellt werden, diese Komponenten zu bestimmen.
Trendkomponente
Die Trendkomponente modelliert die allgemeine zeitliche Entwicklung der Zeitreihe. Dabei werden drei Unterscheidungen vorgenommen: Entweder ist der Trend steigend (zunehmend), fallend (abnehmend) oder horizontal (gleichbleibend). Es existieren verschiedene Verfahren zur Bestimmung der Trendkomponente. Da in der Praxis vielfach von einem linearen Trend ausgegangen wird, kann hier die lineare Regression Anwendung finden, die bereits in Kapitel 3.1.1 vorgestellt wurde. Der lineare Trend ist eine Funktion der Zeit t nach der allgemeinen Geradengleichung
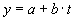 ,
,
wobei der Steigungskoeffizient aussagt, ob eine steigende, fallende oder horizontale Entwicklung vorliegt, je nachdem, ob er positiv, negativ oder Null ist.
Wird der Zeitreihe ein nichtlinearer Trend unterstellt, werden die entsprechenden Parameter ebenfalls mit der Methode der kleinsten Quadrate bestimmt. Fast die gesamte aktuelle Statistik-Software verfügt über numerische Verfahren zur Koeffizientenbestimmung nach dieser Methode.
Zyklische Komponente
Für die Bestimmung der zyklischen Komponente werden entsprechend der zeitlichen Auflösung der vorhandenen Werte (hier: Tage) über mehrere Jahre hinweg Durchschnittswerte gebildet, durch die mittels der Methode der kleinsten Quadrate eine Sinusschwingung gelegt wird. Dabei wird als Periode ein Jahr angenommen, wie es für saisonale Schwankungen üblich ist.
Restkomponente
Die Restkomponente wird nicht wirklich modelliert. Wenn man Aussagen über sie machen könnte, so würden diese Gesetzmäßigkeiten mit in die Trend- oder zyklische Komponente aufgenommen. Wie bereits oben beschrieben, umfaßt die Restkomponente die Abweichungen der Wirklichkeit vom Modell, die bei der Realisierung eines statistischen Prozesses nicht ausbleiben. Sie entspricht damit also dem Fehler des Modells, der zu minimieren versucht wird.
Im Rahmen dieser Arbeit stehen jedoch exogene Zeitreihen zur Verfügung, so daß das univariate klassische Komponentenmodell hier in ein multivariates Verfahren erweitert werden kann. Dazu wird davon ausgegangen, daß sich der Fehler des Modells aus einem erklärbaren und einem unerklärbaren Teil zusammensetzt. Der erklärbare Teil wird als gewichtete Summe exogener Variablen ausgedrückt, wie es auch bei der Regression der Fall ist.
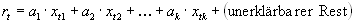
Probleme
Auch bei dem klassischen Komponenten-Ansatz treten verschiedene Probleme auf, die bei der Bewertung der Ergebnisse betrachtet werden müssen:
- Durch die Festlegung der Modellstruktur (additives oder multiplikatives Modell) werden Annahmen über das System getroffen, die i.a. höchstens annähernd der Wirklichkeit entsprechen. Auch wenn dieses Modell mehr Freiheiten bietet als die Regressionsanalyse allein, ist eigentlich ein genaues Wissen um die Systemstruktur nötig, um das Modell optimal anzuwenden.
AR-Modellierung und ARIMA
Im Rahmen der Regressionsanalyse (Kapitel 3.1.1) wurde bereits der Ansatz der multiplen linearen Regression erläutert. Ganz ähnlich ist das Vorgehen bei einem autoregressiven Prozeß (AR-Prozeß), nur das hier statt exogener Indikatoren die gewichtete Summe zeitlich zurückliegender Realisierungen der zu prognostizierenden Variablen verwendet wird. Bei einem "autoregressive-integrated-moving-average"-Prozeß (ARIMA Prozeß, nach Box-Jenkins) handelt es sich um einem stochastischen Prozeß, der autoregressive (AR) und moving-average Prozesse (MA) umfaßt. Als Kurzform verwendet man die Schreibweise ARIMA[p,d,q]-Prozeß. Das ARIMA-Modell vereinigt also folgende Prozesse:
- Einen autoregressiven Prozeß der Ordnung p (AR[p]-Prozeß),
- einen Integrationsprozeß der Ordnung d (I[d]-Prozeß), der nur dann nötig ist, wenn die Zeitreihe zur Erreichung der Stationarität vorher differenziert wurde und
- einen moving-average Prozeß der Ordung q (MA[q]-Prozeß).
Funktionsweise
Bei einem AR[p]-Prozeß wird davon ausgegangen, daß sich die Werte der Zeitreihe als gewichtete Summe der zeitlich zurückliegenden Realisierungen bestimmen lassen. Die Ordung p Î
{0, 1, 2, ...} des Prozesses bezeichnet dabei den größten auftretenden "lag", also die zeitliche Differenz zwischen dem zu prognostizierenden Wert und dem am weitesten zurückliegenden zur Verfügung stehenden Wert. Die allgemeine Form eines AR[p]-Prozesses lautet
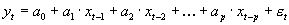
Dabei stellt e
t einen Fehlerterm dar, der die Abweichung vom wahren Wert beschreibt. Für die Summe der Koeffizienten ai (i= 0, 1, ..., p) gilt, daß sie kleiner als Eins sein muß:
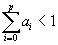
Der I[d]-Prozeß gleicht ggf. einen Differenzenfilter d-ter Ordnung
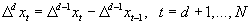
wieder aus.
Ein MA[q]-Prozeß ist ein stochastischer Prozeß, der sich in folgender Form schreiben läßt:
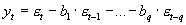
Dabei ist e
t ein White-Noise-Prozeß. Diese Gleichung besagt, daß bei der Prognose die Fehler mit einem bestimmten Gewicht eingehen. Für die Gewichte bi der Gleichung gilt dieselbe Restriktion wie für die ai des AR-Prozesses:
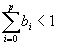
Die Erstellung eines ARIMA[p,d,q]-Modells für eine bestimmte Zeitreihe gliedert sich in vier Phasen:
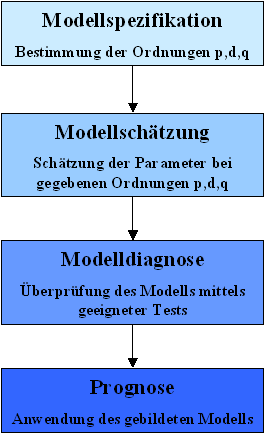
Abbildung .1: Die vier Phasen der Anpassung eines ARIMA[p,d,q]-Modells an eine gegebene Zeitreihe
Die ARIMA[p,d,q]-Modellierung wurde mit GAUSS durchgeführt. Alle vier Schritte in der Modellbildung werden von der Statistiksoftware unterstützt. Verfahren zur Bestimmung der Ordnungen p,d,q über (partielle) Autokorrelationskoeffizienten und zur Findung der freien Parameter finden sich in der Fachliteratur.
Probleme
ARMA- und ARIMA-Prozesse setzen aufgrund ihres autoregressiven Anteils (AR) voraus, daß die Zeitreihe im betrachteten Zeitraum vollständig ist, d.h. keine Fehlwerte aufweist. Für naturwissenschaftliche Meßreihen ist dies im allgemeinen nicht gegeben, wie auch hier für die CO2-Meßreihe. Aus diesem Grund bieten sich zwei Alternativen an: Entweder werden die fehlenden Werte durch ein geeignetes Modell (mathematisch oder neuronal) interpoliert, oder man beschränkt sich bei der Betrachtung auf Abschnitte der CO2-Zeitreihe, die jeweils vollständig sind. Hierbei bietet sich die Zeiträume vom 19.11.94 bis zum 10.12.95 und vom 24.05.94 bis zum 17.11.94 mit 387 bzw. 178 Meßwerten an. Die Anwendung und der Modellvergleich mit den Neuronalen Netzen findet sich in Kapitel XXX (ARIMA).
Neuronale Netze
Einführung
Die Entwicklung Neuronaler Netze (neural networks, NN) begann 1943. Ausgelöst wurde sie durch Warren McCulloch und Walter Pitts im Rahmen ihres Aufsatzes A logical calculus of the ideas immanent in nervous activity. In den frühen Anfängen (1943-1955) stand die Nachbildung realer neuronaler Systeme wie dem Gehirn von Säugetieren mit künstlichen Modellen im Vordergrund. Man spricht daher auch von künstlichen Neuronalen Netzen (artificial neural networks, ANN).
Erst 1986 erlangten die Neuronalen Netze durch die Entwicklung und weite Publikation des Backpropagation-Verfahrens den großen Einfluß, den sie heute haben. Seitdem werden sie in vielen wissenschaftlichen Bereichen vornehmlich zur Prognose, Analyse und Bilderkennung mit Erfolg eingesetzt. Neuronale Netze bieten hier den großen Vorteil, daß sie Algorithmen und Regeln "lernen" können, ohne daß diese vorher explizit bekannt sein müssen.
Die Anwendung Neuronaler Netze gliedert sich in zwei Phasen: Die erste ist die Lern- oder Trainingsphase, in der das Netz Zusammenhänge "lernt", die zweite ist die Recall- oder Applikationsphase, in der das Gelernte genutzt wird, um beispielsweise Prognosen durchzuführen.
Während der Trainingsphase werden dem Netz Trainingsmuster (Input- und Output-Pattern) präsentiert. Durch ein Lernverfahren werden die Variablen des Netzes (Gewichte, siehe unten) so angepaßt, daß der Output des Neuronalen Netzes sich den Output-Pattern möglichst gut annähert. Auf diese Weise werden Zusammenhänge zwischen Input- und Output-Pattern extrahiert, die eine Anwendung des Netzes auch auf solche Muster ermöglichen, die vorher nicht trainiert wurden.
In der Recallphase greift man auf die gelernten Zusammenhänge zurück und präsentiert dem Netz die konkrete Problemstellung, nämlich Input-Pattern, zu denen der Output nicht bekannt ist. Das Netz sollte nun in der Lage sein, den entsprechenden Output zu generieren.
Aufbau Neuronaler Netze
Neuronale Netze bestehen aus vielen miteinander vernetzten sog. Neuronen (Abbildung 3.2). Ein Neuron j besteht aus gewichteten eingehenden Informationskanälen, einer Funktion netj zur Überlagerung der eingehenden Informationen, einer sog. Aktivierungsfunktion aj(net), die aus der überlagerten Information einen Output generiert und einer Outputfunktion oj(a). Die Elemente sind in Abbildung 3.2 dargestellt. Im folgenden werden die einzelnen Schritte der Arbeitsweise eines Neurons erläutert:
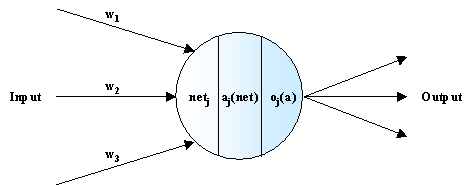
Abbildung .2: Aufbau eines künstlichen Neurons
- Zunächst ermittelt das Neuron seinen Netto-Input, der sich aus dem Output der einzelnen Neuronen der vorigen Schicht ergibt. Dazu werden die eingehenden Informationen mit den Gewichten wi der jeweiligen Verbindungen multipliziert und durch die Eingangsfunktion net zu einem konkreten Wert aggregiert. Für die Modellierung der CO2-Werte sind die eingehenden Informationen xi im allegemeinen reelle Zahlen, es sind aber auch andere Arten von Informationen möglich, wie etwa binäre (ja / nein) Funktionen. Durch Multiplikation der xi mit Gewichten wi kann das Neuron eine Filterung der einzelnen Einflüsse vornehmen, zum Beispiel um unwichtige Informationen durch Nullsetzen der entsprechenden wi auszublenden.
- Aus dem Nettoinput net wird nun der Aktivierungswert des Neurons mit Hilfe der Aktivierungsfunktion a(net) berechnet, die den Nettoinput auf ein festgelegtes offenes Intervall (meist ]0;1[ oder ]-1..+1[) abbildet. Das später erläuterte Netzwerktraining fordert für Netze mit reellem Input, daß die Aktivierungsfunktion stetig differenzierbar ist. Weiterhin ist es sinnvoll, die Nichtlinearität der Funktion zu fordern, da sich andernfalls das Neuron und damit das gesamte neuronale Netz zur einfachen linearen Abbildung reduzieren.
- Im letzten Schritt wird aus der Aktivierung des Neurons die Ausgabe des Neurons berechnet und an die nächste Schicht weitergegeben. Meist handelt es sich bei der Ausgabefunktion o(a) um die Identität, wie auch bei den in dieser Arbeit verwandten Netzen. Aus diesem Grund wird sie einfach als Teil der Aktivierungsfunktion betrachtet.
Vom Neuron zum neuronalen Netzwerk
Um beliebig komplexe Zusammenhänge modellieren zu können, werden viele Neuronen zu sogenannten Neuronalen Netzwerken zusammengefaßt. Je nach Topologie der Vernetzung wird hier von unterschiedlichen Netz(werk)architekturen gesprochen. In dieser Arbeit wurde die sogenannte Feed-Forward Multi-Layer-Perzeptron (FF MLP) Architektur verwandt. Bei dieser Netztopologie sind die Neuronen in mehreren Schichten (Layers) angeordnet, bei der der Output einer Schicht der jeweils nächsten Schicht als Input dient. Der Informationsfluß ist also streng linear von Schicht zu Schicht (Feed-Forward). Die einzelnen Schichten sind dabei voll vernetzt, d.h., es existiert eine Verbindung von jedem Neuron einer Schicht zu jedem Neuron der folgenden Schicht. In Abbildung 3.3 ist dies schematisch dargestellt:
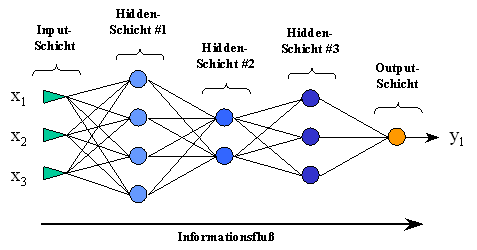
Abbildung .3: Struktur eines fünfschichtigen Feed-Forward-Netzes
Man unterscheidet drei Arten von Neuronen abhängig von ihrer Position im Netzwerk. Die Neuronen der ersten Schicht werden Eingabe- oder Input-Neuronen genannt. Ihnen folgen endlich viele innere Schichten, die dementsprechend Innere- oder Hidden-Schichten genannt werden. Die letzte Schicht stellt den Output des neuronalen Netzes dar und wird deshalb auch Ausgabe- oder Output-Schicht genannt.
Modifikationen der Netzarchitektur
Es existieren verschiedene Erweiterungen der eben vorgestellten Netzarchitektur, die für unterschiedliche Problemklassen eine Verbesserung der Netzgenauigkeit eröffnen. Dazu zählen vor allem die Verwendung einer Vorschicht und sogenannte Shortcut-Verbindungen.
Um die Auswirkungen von extremen Trainingsdaten während der Trainingsphase einzuschränken, wird Neuronalen Netzen eine weitere Schicht von Neuronen vorgeschaltet, die mit der ursprünglichen Input-Schicht (jetzt Hidden #1) einfach vernetzt ist, wie Abbildung 3.4 dargestellt.
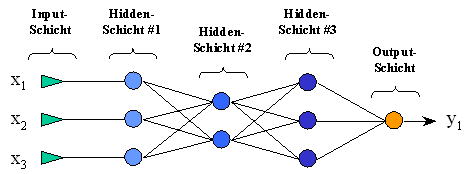
Abbildung .4: Feed-Forward-Netz mit Vorschicht
Dabei wird als Aktivierungsfunktion der Neuronen in der Vorschicht (Hidden #1 in Abbildung 3.4) die logistische Funktion verwandt, so daß Ausreißer auf den Sättigungsbereich der logistischen Aktivierungsfunktion abgebildet werden und der Output des Neurons seinen Charakter als Ausreißer verliert. Da auch die Gewichte an den Verbindungen der Vorschicht zur ersten Hidden-Schicht beim Training verändert werden können, kann das Netz den Umgang mit Ausreißern selbst lernen.
Eine weitere Modifikation der bisher dargestellten Architektur der Feed-Forward-Netze stellen die Shortcut-Verbindungen dar. Hierbei handelt es sich um direkte Verbindungen zwischen zwei nicht benachbarten Schichten, meist der Input- und Output-Schicht. Ist in diesem Fall die Aktivierungsfunktion der Output-Schicht linear, so lassen sich mit Hilfe der Shortcut-Verbindungen lineare Einflüsse modellieren, während der Rest des Netzes (verborgene Schichten) nichtlineare Einflüsse darstellen kann. Theoretisch können Shortcut-Verbindungen zwischen beliebigen nicht benachbarten Schichten bestehen, wie in Abbildung 3.5 dargestellt.
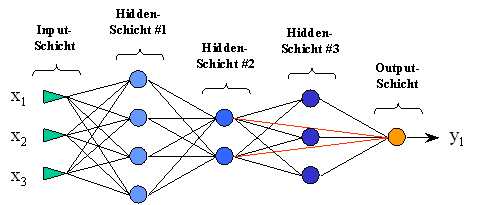
Abbildung .5: Feed-Forward-Netz mit Shortcut-Verbindungen zwischen Hidden-Schicht #2 und Output-Schicht
Training neuronaler Netze
Wie schon eingangs erwähnt, gehört es zu den besonderen Stärken Neuronaler Netze, daß sie Regelmäßigkeiten erkennen können und so den Umgang mit verschiedenen Problemen lernen. Hier soll auf das überwachte Lernen eingegangen werden. Bei dem sogenannten Netztraining wird dabei die Gewichtsmatrix des Neuronalen Netzes in der Weise modifiziert, daß sich der Testfehler des Netzes solange verbessert, bis ein Abbruchkriterium erfüllt ist. Das Lernproblem besteht darin, die durch die Trainingsmenge gegebenen q n-dimensionalen Eingabevektoren xi {i = 1, ..., q} möglichst genau auf die ebenfalls durch die Trainingsmenge gegebenen entsprechenden q m-dimensionalen Ausgabevektoren oi abzubilden. Für das konkrete Problem der Analyse und Prognose von CO2-Werten ist die Dimension der Ausgabevektoren m = 1. Als Maß für die Genauigkeit der Abbildung dient die quadratische Abweichung ENetz der vorgegebenen Ausgabevektoren yi von den durch das Netz bestimmten oi, welche minimiert werden soll:
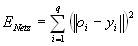
Um die Minimierung des quadratischen Fehlers des Netzes zu erreichen, gibt es verschiedene Lernverfahren. Im folgenden soll nun der wohl populärste Lernalgorithmus vorgestellt werden.
- Der Backpropagation-Lernalgorithmus
Es soll hier lediglich ein Überblick über den Lernalgorithmus gegeben werden. Eine genauere Darstellung mit Herleitung findet sich in der entsprechenden Fachliteratur. Bereits 1974 wurde der später unter dem Namen Backpropagation bekannte Algorithmus in der Dissertation von Paul Werbos entwickelt, seine große Bedeutung erlangte er allerdings erst zwölf Jahre später durch die Arbeiten von Rumelhart und McCulloch (1986).
Der Backpropagation-Algorithmus ist ein sogenanntes Gradientenabstiegsverfahren, d.h., es berechnet den Gradienten der Zielfunktion, hier der Fehlerfunktion, und steigt in Gegenrichtung dazu nach unten, bis ein Minimum erreicht ist. In unserem Fall wird die Minimierung des Fehlers durch Änderung aller Gewichte um einen Bruchteil des negativen Gradienten der Fehlerfunktion realisiert. Die Anwendung des Backpropagation-Verfahrens setzt ein FF-MLP und eine stetig differenzierbare Aktivierungsfunktion, die sogenannte Sigmoide 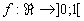 voraus. Für die Aktivierung a eines einzelnen Neurons i ist sie definiert durch:
voraus. Für die Aktivierung a eines einzelnen Neurons i ist sie definiert durch:
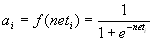
Der Verlauf der sigmoiden Aktivierungsfunktion ist in Abbildung 3.6 graphisch dargestellt.
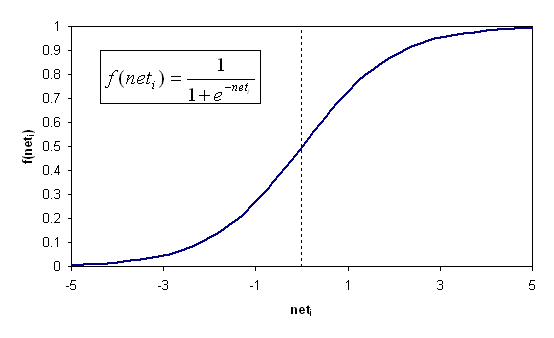
Abbildung .6: Sigmoide Aktivierungsfunktion
Es läßt sich leicht zeigen, daß auch die Ableitung 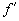 auf dem gesamten Definitionsbereich definiert und stetig ist:
auf dem gesamten Definitionsbereich definiert und stetig ist:
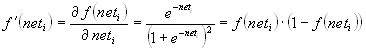
Der Ablauf des Trainings läßt sich folgendermaßen beschreiben: Das Netz wird mit zufälligen Gewichten initialisiert. Ausgehend von einem durch diese Verbindungsgewichte gegebenen Punkt im Fehlergebirge erfolgt eine Modifizierung der Gewichte in der Weise, daß bei jedem Lernschritt ein tieferer Punkt auf der Oberfläche des Fehlergebirges erreicht wird. Dabei wird in Richtung der stärksten Reduzierung des quadratischen Netzfehlers vorgegangen (Gradientenabstieg), womit sich das Verfahren zur Minimumsbestimmung einer nichtlinearen n-dimensionalen Funktion und damit auf ein Optimierungsproblem reduziert. Auf die formale (recht umfangreiche) Darstellung der Herleitung und Lösung wird hier verzichtet (siehe oben).
Das Diagramm aus Abbildung 3.7 zeigt schematisch den Ablauf des Netztrainings, wie es im Rahmen dieser Arbeit eingesetzt wurde:
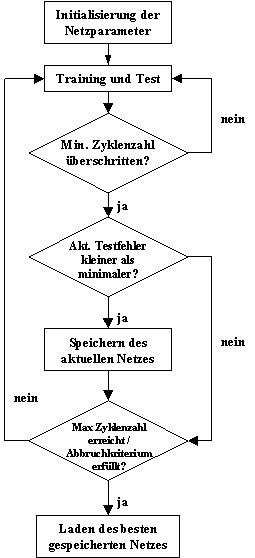
Abbildung .7: Schematischer Ablauf des Netztrainings
Aufgrund der Natur des Backpropagation-Algorithmus wird sich der Fehler auf der Lernmenge asymptotisch einem Minimum nähern. Dabei steigt die Generalisierungsfähigkeit des Netzes zunächst, fällt aber später wieder ab. Um dies zu beobachten, werden die Trainingsdaten in zwei Mengen aufgeteilt: Die Test- und die Lerndaten. Nur die Lerndaten stehen für die Angleichung der Gewichte im Rahmen des Trainings zur Verfügung, während anhand der Testdaten die Generalisierungsfähigkeit des Netzes überprüft wird. Die Aufteilung zeigt Abbildung 3.8.

Abbildung .8: Aufteilung der Wertepaare in Test-, Trainings- und Validierungsmenge (Beispiel)
Nach jedem Lernschritt wird der Netzfehler auf beiden Mengen ausgewertet. Zu einem gewissen Zeitpunkt ist die optimale Generalisierungsleistung erreicht, danach wird sie schlechter. Dies kann an dem Anstieg des Fehlers für die Testmenge beobachtet werden. Ab diesem Punkt lernt das Netz die Lerndaten "auswendig", was aber der Zielsetzung des Lernens, nämlich dem Erkennen von Wirkungszusammenhängen abträglich ist. Aus diesem Grund wird das Training abgebrochen, sobald der Fehler auf den Testdaten über einen bestimmten Prozentsatz (z.B. 20%) des bisherigen Minimums ansteigt.
Es gibt also zwei Abbruchkriterien für das Training: Entweder wird die vorgegebene maximale Zyklenzahl überschritten, oder der Fehler der Testmenge überschreitet sein bisheriges Minimum plus einen frei wählbaren Prozentsatz. Da der zweite Fall in den ersten Zyklen aufgrund der zufälligen Initialisierung der Gewichte vorzeitig eintreten kann, wird weiterhin eine minimale Zyklenzahl vorgeschrieben, vor der das Training nicht beendet wird. Die verschiedenen Abbruchkriterien werden in Abbildung Abbildung 3.9 dargestellt.
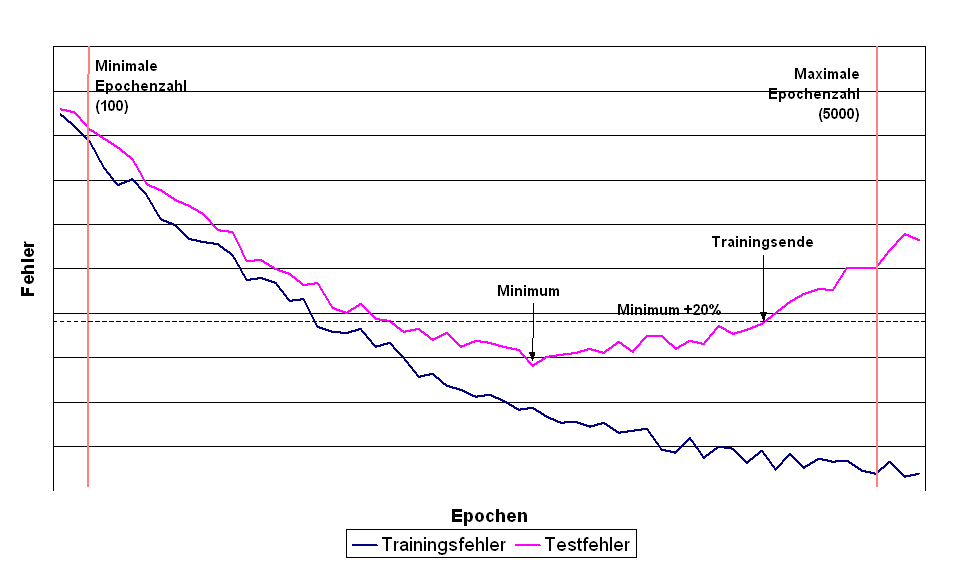
Abbildung .9: Abbruchkriterien und Verlauf von Trainings- und Testfehler während des Netztrainings
Arbeitsumgebung für neuronale Fragestellungen
Der Einsatz Neuronaler Netze im Rahmen dieser Arbeit wurde durch verschiedene Tools ermöglicht, die von der Universität Stuttgart (SNNS) und der Arbeitsgruppe Praktische Informatik der Universität Osnabrück entwickelt wurden (Arbeitsumgebung und Oberfläche zur Zeitreihenanalyse und –prognose).
Der Stuttgarter Neuronale Netze Simulator (SNNS)
"SNNS (Stuttgart Neural Network Simulator) is a simulator for neural networks developed at the Institute for Parallel and Distributed High Performance Systems (Institut für Parallele und Verteilte Höchstleistungsrechner, IPVR) at the University of Stuttgart since 1989."
Der in der Arbeitsgruppe von Andreas Zell entwickelte Simulator deckt die Bereiche Netzwerkgenerierung, Training, Test und Visualisierung der Neuronalen Netze ab, umfaßt jedoch keine Unterstützung bei der Verwaltung von Zeitreihen. SNNS besteht aus vier Hauptkomponenten: Dem Simulatorkern, einer graphischen Benutzeroberfläche, einem batch-Simulator und einem Netzwerkcompiler. Für die Untersuchungen im Rahmen dieser Arbeit wurde im wesentlichen mit der batch-Version von SNNS gearbeitet, die sich über ein in der Arbeitsgruppe Praktische Informatik der Universität Osnabrück entwickeltes Interface und einfache Skripte (Perl 5.0) ansteuern läßt.
Die Möglichkeit, SNNS-Aufrufe in Skripte einzubeziehen, erleichterte die Benutzung des Simulators und ermöglichte ein effizientes Arbeiten. Weiterhin wurden verschiedene Skripte verwendet, die Fehlerbetrachtungen zulassen.
Die Arbeitsumgebung
Unter der Arbeitsumgebung wird das Interface verstanden, mit dessen Hilfe SNNS über Skripte (Perl 5.0) angesprochen werden kann. Sie umfaßt beispielsweise Skripte zur Erstellung der von SNNS verwendeten ASCII-Netzbeschreibungsdatei aus Angaben über Topologie, Anzahl der Neuronen pro Schicht und Modifikationen der Topologie. Aber auch verschiedene Werkzeuge zur Analyse und Evaluierung von Modellzeitreihen nach verschiedenen Fehlermaßen wurden implementiert.
Die Oberfläche
Zu der Arbeitsumgebung wurde 1997 im Rahmen einer Diplomarbeit eine graphische Oberfläche entwickelt, die in erster Linie der Visualisierung der Zeitreihen dient. Dabei können mehrere Zeitreihen gleichzeitig dargestellt werden, auch wenn sie in unterschiedlichen Einheiten und Zeitschritten gegeben sind. Darüber hinaus besteht die Möglichkeit, interaktiv Prognoseläufe vorzunehmen.
Für die vorliegende Arbeit zeigte sie sich besonders nützlich, wenn es darum ging, verschiedene Zeitreihen komfortabel auf einem bestimmten Zeitraum zu vergleichen.
Neuronale Sensitivitätsanalyse
Netzoptimierung: Pruning
Die vielen Freiheiten bei der Festlegung einer Netzwerkarchitektur lassen es sinnvoll erscheinen, es dem Neuronalen Netz selbst zu überlassen, eine geeignete Struktur zu finden. Dabei steht insbesondere eine Minimierung der Architektur im Vordergrund. Aufgrund der vielen freien Parameter, wie Auswahl der Eingabe- und Anzahl der Hidden-Neuronen, sowie der einzelnen Gewichte und Schwellenwerte, kann die Zahl der Trainingspaare nicht ausreichend sein, um sie alle optimal einzustellen. Ist dies der Fall, kann das Netzwerk zwar gut trainiert werden, generalisiert aber schlecht für unbekannte Eingabedaten. Es sind also Verfahren notwendig, die die Komplexität der Neuronalen Netze reduzieren und eine geeignete Netzwerkarchitektur finden. Verfahren dieser Art nennt man Pruning-Verfahren (engl.: pruning = Beschneiden, Ausdünnen), da sie das Netz sukzessive um unwichtige Gewichte und Neuronen reduzieren. Am Ende des Prunings wird jedoch immer das bisher beste Netz verwandt. Es werden zwei Ansätze des Prunings unterschieden: Das Pruning der Gewichte (weight pruning) und das Pruning von Neuronen (Skeletonization oder unit pruning), welches sich weiter aufgliedert in ein Pruning der inneren Neuronen (hidden unit pruning) und ein Pruning der Eingabeneuronen (input unit pruning). Im folgenden werden die Ansätze vorgestellt und ihre Anwendungsmöglichkeiten im Rahmen der Netzwerkoptimierung skizziert.
Weight pruning
Eine Möglichkeit, die Komplexität eines Neuronalen Netzes einzuschränken, besteht darin, die Gewichtsmatrix auszudünnen. Dabei werden einige unwichtige Verbindungen durchtrennt. Das so entstandene Netz hat zwar die gleiche Struktur, ist aber in seinen Verbindungen filigraner geworden. Das hier verwendete Verfahren Optimal Brain Damage wurde 1990 von Le Chun/Denker/Solla in ihrem Artikel Optimal Brain Damage als Ausdünnungsmethode vorgeschlagen.
Die Vorgehensweise ist die folgende: "Optimal Brain Damage [...] versucht, analytisch den Effekt einer Änderung des Parametervektors (Gewichtsvektors) auf die Fehlerfunktion [...] vorherzusagen und diejenige Änderung des Parametervektors durchzuführen, die beim Nullsetzen eines Parameters (Gewichts) die geringste Änderung der Fehlerfunktion bewirkt." Dazu wird die Fehlerfunktion durch eine Taylorreihe um ein lokales Minimum herum angenähert. Eine genauere Darstellung und Herleitung findet sich bei [Zel 96], S.320 ff. und bei [Reh 94], S. 67 ff.
Hidden unit pruning
Dieser Spezialfall der 1989 von Mozer und Smolensky entwickelten Netzwerk-Skelettierung (skeletonization) ist als Fortsetzungsverfahren des Gewichts-Prunings zu verstehen. Ein Neuron der verborgenen Schicht wird aus dem Netz entfernt, indem alle zu und von ihm weisenden Gewichte auf Null gesetzt werden. Dies kann natürlich bereits beim Gewichts-Pruning geschehen, allerdings ist es oftmals sinnvoll, weitere Neuronen zu eliminieren. Dazu werden die Signalflüsse durch die inneren Neuronen verglichen und eine Kreuzkorrelationsanalyse durchgeführt. Eine hohe Korrelation zweier Hidden-Neuronen deutet auf eine Redundanz im Informationsfluß hin und darauf, daß die innere Schicht zu groß ist.
Input unit pruning
Das Pruning von Input-Neuronen läuft nach demselben Schema ab wie das zuvor erklärte hidden unit pruning, allerdings werden hier die Korrelationen der Input-Neuronen analysiert. Für die Bewertung der Inputneuronen gibt es allerdings ein alternatives Verfahren, einen Rangordnungstest. Hierzu wird als Testgröße für jedes Inputneuron der Wert der Zielfunktion berechnet, um den sie sich ändert, wenn man den Input durch seinen Mittelwert ersetzt. Wäre bereits ein lokales Minimum gefunden, so würde die Zielfunktion unter Nutzung aller Inputs kleiner gleich der Zielfunktion bei Nutzung des verkleinerten Inputvektors sein. Die Testgröße wäre somit größer gleich Null und ihr Wert würde den Erklärungsbeitrag dieses speziellen Neurons beschreiben. Das Neuron mit dem kleinsten Erklärungsbeitrag wird entfernt.
Anwendung mehrerer Pruning-Verfahren
Mehrere Pruning-Verfahren können hintereinander ausgeführt werden, um eine Optimierung in verschiedenen Aspekten zu gewährleisten. Allerdings "müssen die drei oben beschriebenen Kompressionsschritte in der angegebenen Reihenfolge angewandt werden."
Im Rahmen dieser Arbeit wurde SNNS um die Funktionalität des mehrfachen Prunings erweitert. Es ist nunmehr möglich, bis zu drei Pruning-Schritte hintereinander durchzuführen. Abbildung 3.10 zeigt den Ablauf des modifizierten Netztrainings.

Abbildung .10: Erweiterung des SNNS-Trainings um mehrfaches Pruning
Somit können alle drei Pruning-Verfahren in das Netztraining eingebunden werden und eine Optimierung der Netzarchitektur in den drei vorgestellten Bereichen durchgeführt werden. Die Anwendung und der Vergleich der Verfahren zur Netzwerkoptimierung finden sich in Kapitel XXX.
Maße für die Analyse- und Prognosegüte
Für die Bewertung von mathematischen oder neuronalen Modellen ist es wichtig, vergleichbare Gütemaße für die Analyse und Prognose zu definieren. Diese werden generell in normierte und nichtnormierte Maße unterschieden. Während nichtnormierte Maße nur dann vergleichbar sind, wenn Analyse- bzw. Prognosezeitraum gleich sind, zeichnen sich normierte Maße durch einen festen Wertebereich (meist [0;1]) und eine generelle Vergleichbarkeit aus.
Ex-ante- und Ex-post-Beurteilung
Um überhaupt den Fehler einer Prognose bestimmen zu können, müssen offenbar die tatsächlichen Werte vorliegen. Bei der Ex-ante-Beurteilung wird die Prognose überprüft, bevor die Werte des Prognosezeitraums vorliegen. Da jedoch eine Beurteilung erst mit den tatsächlichen Werten des Prognosezeitraums stattfinden kann, beschränkt sich die Ex-ante-Beurteilung auf die Modellstruktur.
Im nachhinein, also ex post, kann eine Beurteilung stattfinden, die generell auf der Abweichung des Modellwertes 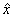 von dem wahren Wert
von dem wahren Wert 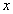 des Prognosezeitraums {t = 1, 2, ..., N} beruht. Diese Differenz
des Prognosezeitraums {t = 1, 2, ..., N} beruht. Diese Differenz 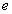 wird auch als Residuum bezeichnet:
wird auch als Residuum bezeichnet:
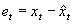
Die hier genannten Maße für Prognosefehler lassen sich auch auf den Fall der Analyse übertragen, deswegen wird im folgenden allgemein von Fehlermaßen gesprochen.
Nichtnormierte Gütemaße
Die in dieser Arbeit verwendeten nichtnormierten Fehler- bzw. Gütemaße können Tabelle 3.1 entnommen werden.
Tabelle .1: Übersicht über die verwendeten nichtnormierten Fehler- bzw. Gütemaße
|
Fehler- bzw. Gütemaß |
Formel |
|
Mittlerer relativer Fehler |
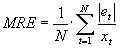
|
|
Mittlerer absoluter prozentualer Fehler |
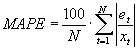
|
|
Summe der quadratischen Fehler (Residuen) |
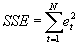
|
|
Wurzel des mittleren quadratischen Prognosefehlers |
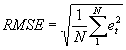
|
Normierte Gütemaße
Im Rahmen dieser Arbeit wurden zwei normierte Gütemaße verwandt, die eine Klassifizierung von Modellen ermöglichen. Eine Übersicht über die verschiedenen Maße findet sich in Tabelle 3.2.
Der Ungleichheitskoeffizient 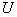 nach Theil vergleicht die Modellergebnisse mit der naiven Prognose, bei der für jeden Prognosewert der Wert des vorigen Zeitpunktes genommen wird. Für eine perfekte Prognose liefert er den Wert Null, wie auch alle anderen Fehlermaße. Generell spricht ein kleinerer Wert für ein besseres Modell. Als Vergleichswert dient die naive Prognose, bei der jeweils der Wert des Vortages verwandt wird. Die naive Prognose erzielt einen Ungleichheitskoeffizienten von eins. Ist
nach Theil vergleicht die Modellergebnisse mit der naiven Prognose, bei der für jeden Prognosewert der Wert des vorigen Zeitpunktes genommen wird. Für eine perfekte Prognose liefert er den Wert Null, wie auch alle anderen Fehlermaße. Generell spricht ein kleinerer Wert für ein besseres Modell. Als Vergleichswert dient die naive Prognose, bei der jeweils der Wert des Vortages verwandt wird. Die naive Prognose erzielt einen Ungleichheitskoeffizienten von eins. Ist 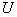 für betrachtete Modelle größer als Eins, so bringt das Modell keine Verbesserung gegenüber dem naiven Verfahren.
für betrachtete Modelle größer als Eins, so bringt das Modell keine Verbesserung gegenüber dem naiven Verfahren.
Der Determinationskoeffizient r2 entspricht dem Quadrat des Korrelationskoeffizienten r zwischen der prognostizierten Zeitreihe und den tatsächlichen Werten. Um r zu berechnen, wird das Produkt der Abweichungen vom Mittelwert der Zeitreihen für die einzelnen Zeitpunkte t aufsummiert und durch beide Standardabweichungen geteilt. Der Wertebereich von r2 ist [0;1], wobei Null keine und Eins eine perfekte Korrelation bedeutet.
Tabelle .2: Übersicht über die verwendeten normierten Fehler- bzw. Gütemaße
|
Fehler- bzw. Gütemaß |
Formel |
|
Ungleichheitskoeffizient von Theil |
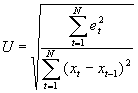
|
|
Determinationskoeffizient |
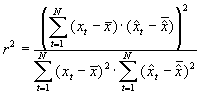
|
Verfahren zur Auswahl exogener Zeitreihen
Die Auswahl geeigneter exogener Zeitreihen ist ausschlaggebend für die Qualität der erstellten Modelle. Dabei möchte man einerseits möglichst viele exogene Datenreihen in Modelle integrieren, um mehr Informationen gewinnen zu können, also das Bestimmtheitsmaß möglichst hoch zu halten. Andererseits ist man bemüht, die Modelle so einfach wie möglich zu halten, sich also auf die wesentlichen Einflußfaktoren zu beschränken. Dies bedeutet aber eine Einschränkung der verwendeten exogenen Zeitreihen. Somit besteht ein Zielkonflikt: Das erstellte Modell soll so einfach wie möglich, aber so komplex wie nötig sein, um eine gute Analyse- bzw. Prognosequalität zu garantieren. Bei der multivariaten Zeitreihenanalyse stellt sich das Problem, aus den möglichen exogenen Datenreihen diejenigen auszuwählen, für die das erstellte Modell den geringsten Fehler liefert. Offenbar sind in einem realen System die Einflüsse der einzelnen Faktoren unterschiedlich groß. In vielen Fällen – wie auch in dieser Arbeit - ist es nicht möglich, alle möglichen Kombinationen exogener Zeitreihen zu überprüfen, da der Rechenaufwand für größere Probleme die vorhandenen Möglichkeiten übersteigt: Die Anzahl Pn,k der Möglichkeiten, aus n vorhandenen exogenen Zeitreihen k für ein Modell auszuwählen, beträgt
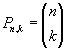 .
.
In dieser Arbeit stehen für die Analyse 22 und für die Prognose 23 exogene Zeitreihen zur Verfügung. Werden nun für die Prognose vier bzw. fünf exogene Zeitreihen ausgewählt, so erhält man
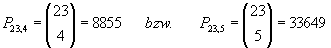
verschiedene Möglichkeiten. Bei einem Zeitaufwand von 50 Sekunden pro Regressionslauf (GAUSS) bzw. 21 Minuten pro Netztraining (SNNS) ergeben sich für fünf exogene Zeitreihen ein zeitlicher Gesamtaufwand von 19,5 Tagen für die Regression und von 490,7 Tagen für das Netztraining. Würde man die Anzahl der möglichen Zeitreihen auf 14 verringern und sich auf vier davon beschränken, ließe sich der Aufwand auf 0,6 bzw. 14,6 Tage reduzieren.
Es ist also insbesondere für neuronale Modelle wünschenswert, im Vorfeld die beste Kombination exogener Zeitreihen für die Modellierung zu bestimmen, ohne alle Möglichkeiten zu testen. Leider kann nur dann sicher behauptet werden, die optimalen Einflußzeitreihen gefunden zu haben, wenn alle anderen Kombinationen getestet wurden. Es ist allerdings möglich, durch geeignete Algorithmen eine "gute", d.h. vielversprechende Kombination zu bestimmen. Im folgenden werden zwei Verfahren vorgestellt und diskutiert, die eine systematische Auswahl ermöglichen.
Auswahl nach Korrelationskoeffizient
Eine Möglichkeit, exogene Zeitreihen für ein Modell auszuwählen, besteht darin, alle verwendeten Zeitreihen nach ihrem Korrelationskoeffizienten zur endogenen Zeitreihe (hier CO2) zu sortieren und ein Modell aus den besten k zu erstellen. Jetzt wird Schritt für Schritt die Zeitreihe mit dem schlechtesten Korrelationskoeffizienten entfernt und durch den nächsten Kandidaten auf der (geordneten) Liste der Kandidaten ersetzt. Verbessert sich das Modell, bleibt er im Modell, ansonsten wird zum bisher besten Modell zurückgekehrt. Wird eine Zeitreihe aus dem Modell entfernt, kommt sie von neuem in die Liste. Wird sie dem Modell hinzugefügt, kann es aber nicht verbessern, wird sie verworfen. Das Verfahren wird solange durchgeführt, bis die Liste leer ist.
Für dieses Verfahren spricht vor allem, daß es sowohl für multivariate mathematische als auch für neuronale Modelle eingesetzt werden kann und bei diesen die Systemstruktur im Verlauf des Verfahrens nicht ändert. Leider kann auch dieses Verfahren nicht die optimale Lösung garantieren: Es ist denkbar, daß eine Zeitreihe verworfen wird, die in Kombination mit anderen Zeitreihen eine bessere Lösung bringen würde Da die Entwicklung dieses Verfahrens noch nicht abgeschlossen ist, kann es noch nicht zu vergleichenden Tests herangezogen werden. Es ist daher nur zur Illustration einer anderen Herangehensweise gedacht.
Auswahl nach Sensitivität
Ein anderes Verfahren bedient sich der (neuronalen) Sensitivitätsanalyse, um geeignete Einflußzeitreihen zu bestimmen. Dazu werden zunächst alle Zeitreihen für ein Modell verwendet. Nach jedem (vollständig abgeschlossenem) Netztraining wird die neuronale Sensitivitätsanalyse durchgeführt und das Inputneuron (die exogene Zeitreihe) mit der geringsten Sensitivität "geprunt", d.h. entfernt. Dies wird sukzessive wiederholt, bis die gewünschte Anzahl exogener Zeitreihen erreicht ist.
Der Vorteil dieses Verfahrens liegt vor allem in seiner kurzen konstanten Laufzeit, es ist jedoch möglich, daß exogene Zeitreihen aufgrund ihres geringen Einflusses zu Anfang entfernt werden, später (bei weniger Inputneuronen) allerdings das Netz verbessern könnten.
Ein weiteres Problem dieses Verfahrens ist seine Strukturinkonsistenz. Während des Ablaufs ändert sich die Netzstruktur (hier: die Anzahl der Inputneuronen) ständig. Aus diesem Grund ist eine Variation der Sensitivität einzelner Inputgrößen möglich.
![]()
![]()