Phase 1: Initial Data Partitioning
Next: Phase 2: Generating
Up: AIDA*
Previous: AIDA*
Before starting a distributed tree search,
each processor must be supplied with a suitable amount of different nodes
which can then be further expanded in parallel.
This could be achieved in logarithmic time, 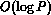 , on
, on 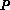 processors,
using a binary divide-and-conquer approach.
However, since communication on a MIMD-machine is usually an order of magnitude more
time-consuming than the node expansion costs
processors,
using a binary divide-and-conquer approach.
However, since communication on a MIMD-machine is usually an order of magnitude more
time-consuming than the node expansion costs ,
AIDA* generates the first few tree levels redundantly on all processors.
In the 15-puzzle, the processors perform an iterative-deepening search,
saving all nodes of the last search frontier in a local node array,
until there are at least
,
AIDA* generates the first few tree levels redundantly on all processors.
In the 15-puzzle, the processors perform an iterative-deepening search,
saving all nodes of the last search frontier in a local node array,
until there are at least 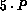 entries.
This gives a sufficient number of subtree roots
(some 10,000 nodes) while not overflowing the memory resources
of our transputer system.
entries.
This gives a sufficient number of subtree roots
(some 10,000 nodes) while not overflowing the memory resources
of our transputer system.
At the end of this phase,
duplicate nodes can be eliminated from the node array.
In our experiments, however, we found that sorting the node array takes too much time.
A total of 30% removed duplicate nodes (cf. [Powley et al., 1993])
at the end of this phase
gave only a 10% reduction of the total nodes, which
did not pay for the increased overhead.
In practice, the first phase is short,
taking less than three seconds (cf., Fig. 4)
on the 1024-node system.
There is neither communication or synchronization involved in this phase.
Volker Schnecke
Mon Dec 19 17:27:56 MET 1994
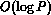 , on
, on 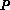 processors,
using a binary divide-and-conquer approach.
However, since communication on a MIMD-machine is usually an order of magnitude more
time-consuming than the node expansion costs
processors,
using a binary divide-and-conquer approach.
However, since communication on a MIMD-machine is usually an order of magnitude more
time-consuming than the node expansion costs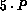 entries.
This gives a sufficient number of subtree roots
(some 10,000 nodes) while not overflowing the memory resources
of our transputer system.
entries.
This gives a sufficient number of subtree roots
(some 10,000 nodes) while not overflowing the memory resources
of our transputer system.