Results

Table 1 shows the performance results of AIDA* for three instances of the 44-Puzzle out of Korf's problem set [1]. All efficiency data is normalized to the performance of an optimal sequential Parix implementation.

  
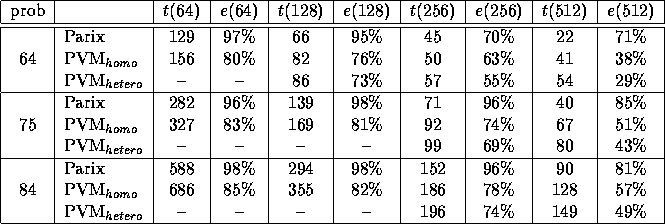
Table 1: The results on the Parsytec GCel

We used two different PVM implementations for our experiments: PVM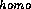 is an 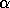-release of a homogeneous PVM version where all tasks are spawned on the transputer nodes of the parallel system. The heterogeneous version, PVM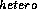, runs on any available hardware, permitting a heterogeneous collection of serial and parallel computers to appear as a single virtual machine. The task management is done by a PVM daemon running on the front-end machine of the parallel system. Both PVM environments are based on Parix.

As can be seen from the table, all three versions scale reasonably well for moderate system sizes. Of course, the implementation on Parix is the fastest. The homogeneous PVM is less efficient, but it performs much better than the heterogeneous version. From the very nature of the heterogeneous PVM, this programming environment cannot be as efficient as the homogeneous implementation, because all messages are checked whether the destination is `within' or `outside' the MPP system.

  
Table 2: Communication time between neighbored processors

In a separate experiment, we benchmarked latency times and communication speed of the three environments. Table 2 shows the communication time between neighbored processors in the GCel system. The messages are not encoded to achieve maximal performance. As can be seen, the setup times of the PVM communication are very high, especially in the heterogeneous version. In our application, only small messages (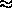 110 byte) are sent, resulting in higher PVM communication overheads for the larger system sizes (Table 1).

  
Table 3: Times to send a message (128 bytes) through all processors

In another experiment we tried to determine the performance loss due to the restriction in the process model. We can't do concurrent work and loadbalancing, because we only have one task on each transputer. So, communication can only take place at certain time intervals, when the search process is interrupted. Table 3 shows the time for sending a message on a ring through all processors of the system with and without a search routine. The time measured without the search routine is the time one would expect, if the communication can be done by a special task concurrent to the node expansion. The delay caused by the search routine increases the average time for a message between `neighbored' processors on the ring from 681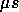 to 2.4 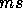on 512 processors when using the same communication frequency like in the real application.