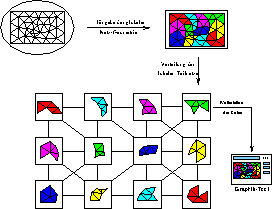
Figure 4: Decomposition algorithm
If we now look at the implementation of the parallel algorithm, two modules have to be constructed. One is the algorithm running on every processor of the parallel system. This algorithm consists of the sequential algorithm operating on a local data set and additional routines for the interprocessor communication. These routines depend on the general logical processor topology, so that the appropriate choice of this parameter is important for the whole parallel algorithm. In Parix this logical topology has to be mapped onto the physical topology which is realized as a two-dimensional grid. For two-dimensional problems there are two possible logical topologies: one-dimensional pipeline and two-dimensional grid. They can be mapped in a canonical way onto the physical topology, so that we have implemented versions of our algorithm for both alternatives.
The second module we had to implement is a decomposition algorithm which reads in the global data structures and calculates a division of the grid and distributes the corresponding local data sets to the appropriate processor of the parallel system. The whole algorithmic structure is shown in figure 4, where we can also see that a given division often requires interprocessor connections, which are not supplied by the basic logical topology. These connections are built dynamically with the so called virtual links of Parix and collected in a virtual topology.

Figure 4: Decomposition algorithm
The essential part of the whole program is the division algorithm which determinates the quality of the resulting distribution. This algorithm has to take different facts into consideration to achieve efficient parallel calculations. First it must ensure that all processors have nearly equal calculation times, because idle processors slow down the speedup. To achieve this it is necessary first to distribute the elements as evenly as possible and then minimize the overhead caused by double calculated nodes and the resulting communications. A second point is the time consumed by the division algorithm itself. This time must be considerably less than that of the actual flow calculation. Therefore we cannot use an optimal division algorithm, because the problem is NP-complete and such an algorithm would take more time than the whole flow calculation. For this reason we have to develop a good heuristic for the determination of a grid division. This task is mostly sequential and as the program has to deal with the whole global data sets we decided to map this process onto a workstation outside the Transputer system. Since nowadays such a workstation is much faster than a single Transputer, this is no patchedup solution, but the performance of the whole calculation even increases.
According to the two versions for the parallel module, we also have implemented two versions for the division algorithm. Since the version for a one-dimensional pipeline is a building block for the two-dimensional case, we present this algorithm first:

The division process is done in several phases here: an initialization phase (0) calculates additional information for each element. The weight of an element represents the calculation time for this special element type (these times are varying because of special requirements of e.g. border elements). The virtual coordinates reflect the position where in the processor topology this element should roughly be placed (therefore the dimension of this virtual space equals the dimension of the logical topology). These virtual coordinates (here it is actually only one coordinate) can be derived from the real coordinates of the geometry or from special relations between groups of elements. An example for the latter case are elements belonging together because of the use of periodic borders. In this case nodes on opposite sides of the calculation domain are strongly coupled and this fact should be reflected in the given virtual coordinates.
Before the actual division an ordering of the elements with a small bandwidth is calculated (phase 1). This bandwidth is defined as the maximum distance (that is the difference of indices in the ordering) of two adjacent elements. A small bandwidth is a requirement for the following division step. Finding such an ordering is again a NP-complete problem, so we can not get an optimal solution. We use a heuristic, which calculates the ordering in two steps. First we need a simple method to get an initial ordering (a). In our case we use a sorting of elements according to their virtual coordinates. In the second step (b) this ordering is optimized e.g. by exchanging pairs of elements if this improves the bandwidth until there is no more exchanging possible.
With the received ordering and the element weights the actual division is now calculated. First the elements are divided into ordered parts with equal weights (phase 2). Then this division is analysed in terms of resulting borders and communications and is optimized by reducing border length and number of communication steps by exchanging elements with equal weights between two partitions (phase 3).
If we now want to construct a division algorithm for the two-dimensional grid topology we can use the algorithm described above as a building block. The resulting algorithm has the following structure:

The only difference between the one and the two-dimensional version of the initialization phase is the number of virtual coordinates which here of course is two. Phase 3 has the same task which is much more complex in the two-dimensional case. The middle phase here is a two stage use of the one-dimensional strategy, where the grid is first cut in the x-dimension and then all pieces are cut in the y-dimension. This strategy can be substituted by a sort of recursive bisectioning, where in every step the grid is cut into two pieces in the larger dimension and both pieces are cut further using the same strategy.