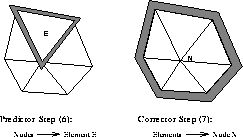
Figure 1: Balance areas
This section gives a brief description of the equations which are necessary for the parallel flow calculations.
For our flow calculations on unstructured grids with the finite element method we use Navier-Stokes Equations for viscous flow and Euler Equations for inviscid flow. The Navier-Stokes (Euler) Equations can be written in the following form,
where U, F and G are 4-dimensional vectors. U describes mass, impulses and energy, F and G are flow vectors. The flow vectors are different for the Euler and Navier-Stokes equations, in both cases we have to add two equations to close the system.
The solution of these differential equations is calculated with an explicit Taylor-Galerkin two step algorithm. Therefore, at first a Taylor series in time is developed, which looks like
and in other form
The expression in parenthesis can be seen as
If we take no consideration of the -term from equation (3) we achieve
With equation (1) and a replacement of the time derivation of equation (4) and (5) the two steps of the Taylor-Galerkin algorithm are:
and
The differential equations can be expressed in a weighted residual formulation using triangular finite elements with linear shape functions. Therefore, in the first step the balance areas of the convective flows for one element have to be calculated on the nodes of each element. In the second step the balance area for one node is calculated with the help of all elements which are defined with this node. A pictorial description of these balance areas of the two steps is given in figure 1.
The calculation with the finite element method, which divides the calculation area into triangles, leads to the characteristic summation of the element matrices into the global mass matrix M and to the following equation system
where is the abbreviation for the summation of the right hand sides of equations (7) for all elements. The inversion of the Matrix M is very time consuming and therefore we use, with the help of the so called lumped mass matrix , the following iteration steps:
For the determination of three iteration steps are sufficient. If we consider stationary flow problems only the initial iteration has to be calculated.
The time step must be adjusted in a way where the flow of information does not exceed the boundaries of the neighbouring elements of a node. This leads to small time steps if instationary problems are solved (in the case of stationary problems we use a local time step for each element). In both cases the solution of a problem requires the calculation of many time steps, so that the steps (6), (7), (9) and (10) are carried out many times for a given problem. The resulting structure for the algorithm is a loop over the number of time steps, where the body of this loop consists of one or more major loops over all elements and some minor loops over nodes and boundaries (major and minor in this context reflects the different runtimes spent in the different calculations).
Another important characteristic of this method is the use of unstructured grids. Such grids are characterized by various densities of the finite elements for different parts of the calculation area. The elements of an unstructured grid differ in both size and number of adjacent elements, which can result in a very complex grid topology. This fact is one main reason for the difficulties arising in constructing an efficient parallel algorithm.
The main advantage of unstructured grids is their ability to adapt a given flow. To get a high resolution of the details of a flow, the density of the grids must only be increased in the interesting parts of the domain. This leads to a very efficient use of a given number of elements. One problem arising in this context is the fact that in most cases the details of a flow are the subject of investigations, so that it is impossible to predict the exact regions, where the density of the grid has to be increased. A solution of this problem is a so called adaptive grid refinement, where the calculations start with a grid with no or little refinements. As the calculations proceed, it is now possible to detect regions, where the density of the grid is not sufficient. These parts of the grid will then be refined and the calculations proceed with the refined grid. These refinement step is repeated until the quality of the solution is sufficient.