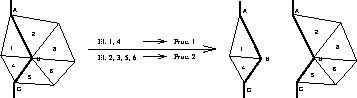
Figure 2: Grid division
If we are looking for parallelism in this algorithm we observe that the results of one time step are the input for the next time step, so the outer loop has to be calculated in sequential order. This is not the case for the inner loops over elements, nodes and boundaries which can be carried out simultaniously. So the basic idea for a parallel version of this algorithm is a distributed calculation of the inner loops. This can be achieved by a so called grid division, where the finite element grid is partitioned into sub grids. Every processor in the parallel system is then responsible for the calculations on one of these sub grids. Figure 2 shows the implication of this strategy on the balance areas of the calculation steps.
The distribution of the elements is non overlapping, whereas the nodes on the border between the two partitions are doubled. This means that the parallel algorithm carries out the same number of element based calculations as in the sequential case, but some node based calculations are carried out twice (or even more times, if we think of more complex divisions for a larger number of processors). Since the major loops are element based, this strategy should lead to parallel calculations with nearly linear speedup. One remaining problem is the construction of a global solution out of the local sub grid solutions. In the predictor step the flow of control is from the nodes to the elements, which can be carried out independently. But in the corrector step we have to deal with balancing areas which are based on nodes which have perhaps multiple incarnations. Each of these incarnations of a node sums up the results from the elements of its sub grid, whereas the correct value is the sum over all adjacent elements. As figure 3 shows, the solution is an additional communication step where all processors exchange the values of common nodes and correct their local results with these values.
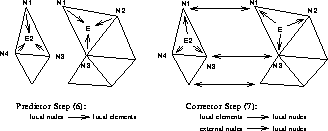
Figure 3: Parallel calculations
This approach, where the sequential algorithm is used on distributed parts of the data sets and where the parallel and the sequential version are arithmetically equivalent, is usually described with the key word data decomposition. Other domain decomposition approaches have to deal with numerically different calculations in different parallelel cases, and have to pay special attention to numerical stability. In the case of implicit algorithms it is common to make a division of the grid nodes, due to the structure of the resulting system of linear equations, which have to be solved in parallel. The main advantage of the explicit algorithm used here is the totally local communication structure, which results in a higher parallel efficiency, specially for large numbers of processors.
This structure implies a MIMD architecture and the locality of data is exploited best with a distributed memory system together with a message passing environment. This special algorithm has a very high communication demand, because in every time step for every element loop an additional communication step occurs. An alternative approach in this context is an overlapping distribution, where the subgrids have common elements around the borders (see [5]). This decreases the number of necessary communications but leads to redundant numerical calculations. We decided to use non-overlapping divisions for two reasons: First they are more efficient for large numbers of subgrids (and are therefore better suited for massively parallel systems), and the other reason is that we want to use adaptive grids. The required dynamic load balancing would be a much more difficult task for overlapping subgrids. The only drawback of our approach is that to obtain high efficiencies a parallel system with high communication performance is required, so it will not work e.g. on workstation clusters. Our current implementation is for Transputer systems and uses the Parix programming environment, which supplies a very flexible and comfortable interprocessor communication library. This is necessary if we think of unstructured grids which have to be distributed over large processor networks leading to very complex communication structures.